В равносторонний трапеции с углом 60 градусов высота, проведенная из вершины тупого угла, делит большую основу для отрезки 4 см и 10 см. Найдите периметр трапеции.
Дано: АВСД - равнобедренная трапеция, ВН, ВМ - высоты АВСД, ∠ВАД=60°, АН=4 см, НД=10 см.
Найти:
Решение: Рассмотрим ΔАВН и ΔМСД - прямоугольные по определению. Поскольку ∠ВАД=∠СДМ=60° и АВ=СД - по свойству равнобедренной трапеции, то ∠АВН=∠МСД=30° и АВ=2АН - по свойству прямоугольного треугольника (катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы); АВ=2×4=8(см) и ВН=СМ - как высоты, тогда ΔАВН=ΔМСД - по двум сторонам и углу между ними ⇒ АН=МД=4 см, значит НМ=НД-МД=10-4=6 (см)
НВСД - прямоугольник по признаку (ВН=СМ, все углы - прямые), тогда НМ=ВС=6 (см) - по свойству прямоугольника.
В равнобедренном треугольнике ABC угол В равен 30°, AB=BC=6, проведены высота CD треугольника ABC и высота DE треугольника BDC. Найдите BE.
——————————
ответ: 4,5 (ед. длины)
Объяснение:
Из ∆ ВDC катет DC противолежит углу 30° ⇒ DC=ВС:2= 6:2=3 (свойство).
Высота прямоугольного треугольник, проведенная к гипотенузе, делит его на треугольники, подобные друг другу и исходному треугольнику. Сумма острых углов прямоугольного треугольника 90°.
В равносторонний трапеции с углом 60 градусов высота, проведенная из вершины тупого угла, делит большую основу для отрезки 4 см и 10 см. Найдите периметр трапеции.
Дано: АВСД - равнобедренная трапеция, ВН, ВМ - высоты АВСД, ∠ВАД=60°, АН=4 см, НД=10 см.
Найти: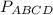
Решение: Рассмотрим ΔАВН и ΔМСД - прямоугольные по определению. Поскольку ∠ВАД=∠СДМ=60° и АВ=СД - по свойству равнобедренной трапеции, то ∠АВН=∠МСД=30° и АВ=2АН - по свойству прямоугольного треугольника (катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы); АВ=2×4=8(см) и ВН=СМ - как высоты, тогда ΔАВН=ΔМСД - по двум сторонам и углу между ними ⇒ АН=МД=4 см, значит НМ=НД-МД=10-4=6 (см)
НВСД - прямоугольник по признаку (ВН=СМ, все углы - прямые), тогда НМ=ВС=6 (см) - по свойству прямоугольника.
ответ: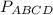 = 36 см
= 36 см
В равнобедренном треугольнике ABC угол В равен 30°, AB=BC=6, проведены высота CD треугольника ABC и высота DE треугольника BDC. Найдите BE.
——————————
ответ: 4,5 (ед. длины)
Объяснение:
Из ∆ ВDC катет DC противолежит углу 30° ⇒ DC=ВС:2= 6:2=3 (свойство).
Высота прямоугольного треугольник, проведенная к гипотенузе, делит его на треугольники, подобные друг другу и исходному треугольнику. Сумма острых углов прямоугольного треугольника 90°.
Угол BСD=90°-∠DBC=90°-30°=60°, угол ЕDC=30°.
CD - гипотенуза прямоугольного ∆ СЕD, катет ЕС противолежит углу 30°,⇒ ЕС=СD:2=3:2=1,5 ⇒
ВЕ=6-1.5=4,5
Или:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией катета на неё.
СD²=BC•EC. Из найденного СD=3.
3²=6•CE ⇒ CE=1,5 a BE=BC-CE=6-1,5=4,5