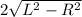На клетчатой бумаге с размером клетки 0, 5 х 0, 5 см изображён шестиугольник. Найди его площадь ​

Объяснение:

    456 . В задачі Можливі два випадки :

   1) Зовнішній кут ∠BCD = 118° лежить при основі рівнобедреного

      ΔАВС  :    АВ = ВС . Тоді ∠А = ∠С = 180° - 118° = 62° ;

     ∠В = 180° - 2* ∠А = 180° - 2* 62° = 56° .

   2)  Зовнішній кут ∠DBC = 118° лежить при основі рівнобедреного          ΔАВС  :    АВ = ВС . Тоді  ∠АВС = 180° - 118° = 62° ;

∠А = ∠С = ( 180° - ∠АВС ) : 2 = ( 180° - 62° ) : 2 = 59° .

В  -  дь : задача має два розв"язки :

                   1) 62° , 62° , 56° ;    2) 62° , 59° , 59° .

    460 . Нехай в ΔАВС  ∠А : ∠В : ∠С = 7 : 8 : 9  і  їх градусні міри

  становлять  ∠А = 7х° , ∠В = 8х° , ∠С = 9х° . Позначимо відповідні

  їм зовнішні кути α , β , γ . За власт. зовнішніх кутів тр - ника

   α = 8x° + 9x° = 17x° ;   β = 7x° + 9x° = 16x° ;  γ = 7x° + 8x° = 15x° .

   Тому відношення  α : β : γ = ( 17x ) : ( 16x ) : ( 15x ) = 17 : 16 : 15 .

   В - дь :   17 : 16 : 15 .

Объяснение:

Дано: Окр.О,R;

MO = L

MB₁, MB₂, A₂A₁ - касательные.

Найти: Р (ΔА₁МА₂)

1. Рассмотрим ΔОМВ₁.

Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОВ₁ ⊥ МВ₁ ⇒ ΔОМВ₁ - прямоугольный.

По теореме Пифагора найдем МВ₁ :

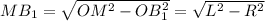
2. Отрезки касательных к окружности, проведённые из одной точки, равны.

⇒ МВ₁ = МВ₂ =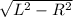

3. Рассмотрим ΔА₁МА₂

Р (ΔА₁МА₂) = А₂М + МА₁ + А₁А₂

А₁А₂ = А₁С + СА₂

А₂С = А₂В₂ ;  СА₁ = А₁В₁ (отрезки касательных)

Тогда:

Р (ΔА₁МА₂) = А₂М + МА₁ + А₁С + СА₂ = А₂М + МА₁ + А₁В₁ + А₂В₂

А₂М + А₂В₂ = МВ₂

МА₁ + А₁В₁ = МВ₁

⇒ Р (ΔА₁МА₂)  = МВ₂ + МВ₁ =