На координатной плоскости даны фигуры A, B и C. [2б.] а) при повороте фигура А перешла в фигуру В. Найдите направление и угол поворота;
б) при симметрии фигура А перейдет в фигуру С. Напишите уравнение оси симметрии.

Решение:
1) Треугольник ОВА равнобедренный с катетами 12√2
тогда: ОА=√(288+288)=24
2) Обозначим точки касания В и С тогда треугольник АОВ прямоугольный, найдем катет АВ:
АВ=√(48-36)=2√3
Найдем высоту этого треугольника:
S=0,5AB*OB=0,5*6*2√2=6√2
h=2S/AO=12√2/4√2=3
следовательно хорда ВС=2h=6
Тогда треугольник ОВС равносторонний и угол ВОС=60°
Угол ВАС=360°-180°-60°=120°
3) Так как диагонали ромба точкой пересечения К делятся пополам и взаимно-перпенидкулярны, то радиус окружности проведенный в точку касания К перпендикулярен АС, следовательно АС - касательная.
4) Вершины этого четырехугольника разделили окружность на дуги равные:
х+2х+8х+7х=360°
18х=360°
х=20°
Величины вписанных углов равны половине дуги на которую они опираются следовательно углы четырехугольника равны:
30° , 100°, 150° , 80°
5) Диаметр окружности равен 50, следовательно радиус равен 25    

Второй случай решения состоит в том, что общий угол у ромба и у треугольника находится при основании треугольника.

Имеется рисунок (вложение)

известно, что AC=12, BC=9, AB = 9.

Из свойства равнобедренного треугольника следует, что угол BAC равен углу ACB. (1)

Из параллельности сторон в параллелограмме (а ромб является частным случаем параллелограмма) следует, что угол BDE равен углу DAF, а угол DAF равен углу EFC (2).

AE - биссектриса угла ВАС (из свойств ромба). По теореме о биссектрисах

,

откуда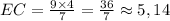 

Так как этот треугольник - равнобедренный (из 1 и 2), то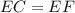 , где EF - сторона ромба.