На продолжении стороны ab равнобедренного треугольника abc с основанием ac отметили точку d так что ad равно ac. находящийся между точками b и d найдите величину угла adc если угол abc равен 44 градусов
Как показано на рисунке 611 — AF == AD = AD/2; BC == AF == FD = AD/2.
Теорема такова: если отрезок, проведённый из двух сторон — равен половине третьей стороны, то этот отрезок — средняя линия.
Как мы видим, на стороне AM, центр — B, на стороне AD, центр — F, а на стороне MD, центр — C. Тоесть отезок FC — проведён с центров двух сторон, тоесть — она средняя линия.
Отметим ещё то, что средняя линия параллельна своей противоположной стороне(факт), тоесть: BC║AD.
FC — также средняя линия, тоесть — она равна половине своей противоположной стороны, тоесть: AM = 10 ⇒ CF = 10/2 = 5.
Вывод: CF = 5.
1.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2 ⇒ BC = 4.
Для вычисления площади прямоугольного треугольника — нам надо знать 2 катета(гипотенуза к чёрту не нужна).
А чтобы найти катет AC — зная первый катет, и гипотенузу — используем простейшую теорему Пифагора:
Формула вычисления площади прямоугольного треугольника:
Внимание! Эта формула работает только с прямоугольным треугольником, так как прямоугольный треугольник имеет один прямой угол.
Вычисление площади обычного произвольного треугольника — содержит альтернативную формулу!
2.
Так как один из острых углов равен 45°, то второй острый угол равен: 90-45 = 45° ⇒ <M == <N = 45° ⇒ KM == KN = 4.
Зная 2 катета — найдём гипотенузу NM:
Вывод: NM = 5.66.
3.
Формула вычисления боковой стороны, зная угол, противолежащий основанию, и основание: .
4.
Формула вычисления биссектрисы, проведённую через острый угол в прямоугольном треугольнике такова:
5.
Формула вычисления диагонали CD — зная 2 стороны:
Формула вычисления любой стороны прямоугольника, зная диагональ:
АВ=ВС, т.к. треугольник равнобедренный, а АС - основание. ВК=2, АК=8, тогда, АВ=10. Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов. АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16. В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6. Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.
10.
Как показано на рисунке 611 — AF == AD = AD/2; BC == AF == FD = AD/2.
Теорема такова: если отрезок, проведённый из двух сторон — равен половине третьей стороны, то этот отрезок — средняя линия.
Как мы видим, на стороне AM, центр — B, на стороне AD, центр — F, а на стороне MD, центр — C. Тоесть отезок FC — проведён с центров двух сторон, тоесть — она средняя линия.
Отметим ещё то, что средняя линия параллельна своей противоположной стороне(факт), тоесть: BC║AD.
FC — также средняя линия, тоесть — она равна половине своей противоположной стороны, тоесть: AM = 10 ⇒ CF = 10/2 = 5.
Вывод: CF = 5.
1.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2 ⇒ BC = 4.
Для вычисления площади прямоугольного треугольника — нам надо знать 2 катета(гипотенуза к чёрту не нужна).
А чтобы найти катет AC — зная первый катет, и гипотенузу — используем простейшую теорему Пифагора:
Формула вычисления площади прямоугольного треугольника: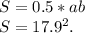
Внимание! Эта формула работает только с прямоугольным треугольником, так как прямоугольный треугольник имеет один прямой угол.
Вычисление площади обычного произвольного треугольника — содержит альтернативную формулу!
2.
Так как один из острых углов равен 45°, то второй острый угол равен: 90-45 = 45° ⇒ <M == <N = 45° ⇒ KM == KN = 4.
Зная 2 катета — найдём гипотенузу NM:
Вывод: NM = 5.66.
3.
Формула вычисления боковой стороны, зная угол, противолежащий основанию, и основание: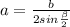 .
.
4.
Формула вычисления биссектрисы, проведённую через острый угол в прямоугольном треугольнике такова:
5.
Формула вычисления диагонали CD — зная 2 стороны: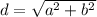
Формула вычисления любой стороны прямоугольника, зная диагональ: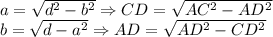
Формула вычисления площади прямоугольника: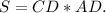
ВК=2, АК=8, тогда, АВ=10.
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов.
АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16.
В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6.
Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.