на прямой а от точки а в одном направлении отложены два отрезка аб и ац так что фц больше аб от точки ц на этой прямой отложите такой отрезок це.чтобы ац равно бе сравните отрезки це и аб нужно решение

30° и 60°

Объяснение:

1) Пусть О - точка пересечения диагоналей трапеции.

ΔВОС подобен ΔАОD, при этом коэффициент подобия k равен:

k = AD : ВС = 2 : 1 = 2, т.к., согласно условию, АD = 2BC.

2) Из подобия треугольников следует, что точкой О:

а)   диагональ ВD делится на 2 отрезка:

ВО = BD : 3 = 3√3 : 3 = √3

ОD = BD : 3 · 2 = 3√3 : 3 · 2 = 2√3 ;

б) диагональ АС делится на 2 отрезка:

СО = АС : 3 = 3 : 3 = 1

АО = 3 : 3 · 2 = 2.

3) Так как BD⊥АС, то треугольники ВОС и АОD - прямоугольные.

tg∠CBD = СО : ВО = 1/√3 = √3/3

∠CBD = arctg (√3/3)  = 30°

∠ВСА = 90° - ∠CBD = 90° - 30° = 60°.

∠ВDА = ∠CBD = 30° - как углы внутренние накрест лежащие;

∠DАС = ∠ВСА = 60° - как углы внутренние накрест лежащие.

ответ: диагонали трапеции образуют с её основаниями углы 30° и 60°.

(см. объяснение)

Объяснение:

Первая система уравнений:

Раскроем скобки:

В первой строке вынесем xy за скобки, а из второй выразим x+y:

Теперь подставим x+y из второго уравнения в первое:

Делаем замену вида :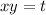

Решим это уравнение:

Получили две сильно упрощенные системы:

            или            

Для первого случая:

Для второго случая:

Итого исходная система имеет четыре решения:

Система уравнений решена!

Вторая система уравнений:

Умножим первое уравнение на 5, а второе на 14:

Теперь приравняем левые части:

Выполним преобразования:

Теперь есть два подхода к решению:

Делим все уравнение на y², вводим замену вида и решаем уравнение . После чего получаем, что или . Дальнейшие действия очевидны.Разложим уравнение на множители, заметив, что .

Я рекомендую пользоваться первым .

Итак, имеем две системы:

            или            

Для первого случая:

Для второго случая:

Итого исходная система имеет четыре решения:

Система уравнений решена!

Задание выполнено!