Диагонали квадрата равны. Квадрат - это ромб, а площадь ромба равна половине произведения его диагоналей. Можно применить формулу площади ромба для нахождения площади квадрата:
S = (дм²)
Диагональ квадрата образует с двумя его сторонами прямоугольный треугольник, причем диагональ при этом является гипотенузой этого треугольника.
Пусть сторона квадрата x дм, тогда по теореме Пифагора:
32дм²
Объяснение:
Диагонали квадрата равны. Квадрат - это ромб, а площадь ромба равна половине произведения его диагоналей. Можно применить формулу площади ромба для нахождения площади квадрата:
S =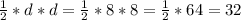 (дм²)
(дм²)
Диагональ квадрата образует с двумя его сторонами прямоугольный треугольник, причем диагональ при этом является гипотенузой этого треугольника.
Пусть сторона квадрата x дм, тогда по теореме Пифагора:
x² + x² = 8²
2x² = 64
x² = 32
x = √32 = √16*2 = 4√2 (дм)
Площадь квадрата x², то есть площадь равна 32дм²
а) 0,5:1
б) 100:126:169
(3+4+8)=180°; a=180/15=12
ZA=3*12=36°
ZB=12*4=48°
ZC=12*8=96
a=100
b=126
c=169
Объяснение:
︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎ ︎