1)Сторона квадрата это два радиуса, то есть a = 2r = 2 * 5 = 10
По теореме Пифагора, диагональ = =, где а - сторона квадрата
2) Сумма улов n-угольника s = 180(n - 2)
1600 = 180(n - 2);
1600 = 180n - 360;
1960 = 180n;
196 = 18n;
n = 10,8 а так как n не является натуральным числом то такого многоугольника не существует
3)Так ромб частный случай паралеллограмма то его диагонали точкой пересечения делятся пополам, а свойству ромба его диагонали перпендикулярны, тогда по теореме Пифагора a =
(a - сторона ромба )
По свойству ромба все его стороны равны тогда P ромба = 4a
Такие задачи решать не нужно в классическом виде. Они решаются так - 1) длина окружности и радиус линейно зависимы . (т.е. при изменении одной величины другая изменяется в столько же раз) 2) у площади и радиуса зависимость квадратичная (т.е. при изменении радиуса площадь изменяется в квадрате, а при изменении площади радиус изменяется в квадратном корне)
3) значит, при изменении длины окружности радиус изменяется во столько же раз, а площадь в квадрате. Т.е. при уменьшении окружности в 3 раза радиус тоже уменьшается в 3 раза, а площадь в 3² =9 раз.
Много написано, но это для полного пояснения. Там решение в одну фразу.
1)Диагональ квадрата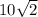
2)Такого правильного многоугольника не существует
3)Периметр ромба 60
Объяснение:
1)Сторона квадрата это два радиуса, то есть a = 2r = 2 * 5 = 10
По теореме Пифагора, диагональ =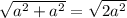
=
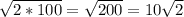, где а - сторона квадрата
2) Сумма улов n-угольника s = 180(n - 2)
1600 = 180(n - 2);
1600 = 180n - 360;
1960 = 180n;
196 = 18n;
n = 10,8 а так как n не является натуральным числом то такого многоугольника не существует
3)Так ромб частный случай паралеллограмма то его диагонали точкой пересечения делятся пополам, а свойству ромба его диагонали перпендикулярны, тогда по теореме Пифагора a =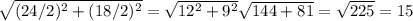
(a - сторона ромба )
По свойству ромба все его стороны равны тогда P ромба = 4a
= 4 * 15 = 60
1) длина окружности и радиус линейно зависимы . (т.е. при изменении одной величины другая изменяется в столько же раз)
2) у площади и радиуса зависимость квадратичная (т.е. при изменении радиуса площадь изменяется в квадрате, а при изменении площади радиус изменяется в квадратном корне)
3) значит, при изменении длины окружности радиус изменяется во столько же раз, а площадь в квадрате. Т.е. при уменьшении окружности в 3 раза радиус тоже уменьшается в 3 раза, а площадь в 3² =9 раз.
Много написано, но это для полного пояснения. Там решение в одну фразу.