1)Треугольники подобны ⇒ и у другого треугольника стороныотносятся как 3х/4х/5х. Большая сторона - 5х, и она равна 15.
15=5х
х=3
тогда первая сторона 3х=9, вторая 4х=12
Периметр равен:9+12+15=36
ответ:36
2)Больший катет лежит против большего отрезка гипотенузы. По свойству катет в прямоугольном треугольнике есть среднее геометрическое между гипотенузой (16+9=25см) и его проекцией на гипотенузу (16см)
1)Треугольники подобны ⇒ и у другого треугольника стороныотносятся как 3х/4х/5х. Большая сторона - 5х, и она равна 15.
15=5х
х=3
тогда первая сторона 3х=9, вторая 4х=12
Периметр равен:9+12+15=36
ответ:36
2)Больший катет лежит против большего отрезка гипотенузы. По свойству катет в прямоугольном треугольнике есть среднее геометрическое между гипотенузой (16+9=25см) и его проекцией на гипотенузу (16см)
х=√(25*16)=20см
ответ:20см
3)Рисунок внизу.
В ΔABD по теореме косинусов:
cosABC=(AB²+BD²-AD²)/(2AB*BD)=(16+1-12,25)/(2*4*1)=4,75/8
В ΔABC по теореме косинусов:
AC²=AB²+BC²-2*AB*BC*cosABC=16+256-2*4*16*4,75/8=196
AC=14
ответ:14
a) Модуль АМ=5.3 cм
б) (АВ-АС)*ВС= {0; 0; 0}
в) ∠ВДА=60°
г) векторы не колинеарны
Объяснение:
a) М(-0,5;1;2) СЕРЕДИНА ОТРЕЗКА ВС
АМ(-4,5;2;2)
Модуль АМ=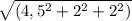
=5.3 cм
б) АВ-АС=(-6;1;2)-(-3;3;2)=(-3;-2;0)
(АВ-АС)*ВС=(-3;-2;0)*(3;2;0)= {0; 0; 0}
i j k
ax ay az
bx by bz
=
i j k
-3 -2 0
3 2 0
= i ((-2)·0 - 0·2) - j ((-3)·0 - 0·3) + k ((-3)·2 - (-2)·3) =
= i (0 - 0) - j (0 - 0) + k (-6 + 6) = {0; 0; 0}
в) Из ΔВДА найдем ∠ВДА по теореме косинуса, сторона лежащая напротив этого угла АВ
АВ^2=BD^2+AD^2-2BD*ADcos∠ВДА
Модуль АВ(-6;1;2)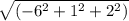
=6,4 cм
Модуль ВС(3;2;0)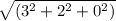
=3,6 cм
Модуль АД(-1;2;7)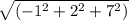
=7,35 cм
6.4^2=3.6^2+7,35^2-2*3.6*7,35cos∠ВДА
cos∠ВДА=0,5; ∠ВДА=60°
г) Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Векторы АВ(-6;1;2) АС(-3;3;2) АД (-1;2;7) имеют общее начало т А
Отношение координат разное (2; 1/3; 1) Поэтому векторы не колинеарны