66° и 42°
Объяснение:
Дано: Окр.О;
АВСD - вписанный четырехугольник;
АС ∩ BD = M; AB ∩ BC = N;
∠АMD = 108°; ∠AND = 24°.
Найти: ∠АBD и ∠BDC.
1.
⇒
(1)
(2)
Из (2) выразим дугу AD и подставим в (1):
2. Теперь можем найти искомые углы.
∠B = 53°; S=900мм²
Поперечный разрез паза имеет форму равнобедренной трапеции.
Нам надо найти угол В и площадь данной трапеции.
1. Угол найдем из ΔВАС.
Рассмотрим ΔВАС - прямоугольный.
По таблице найдем угол:
∠В ≈ 53°
2. Найдем площадь трапеции:
66° и 42°
Объяснение:
Дано: Окр.О;
АВСD - вписанный четырехугольник;
АС ∩ BD = M; AB ∩ BC = N;
∠АMD = 108°; ∠AND = 24°.
Найти: ∠АBD и ∠BDC.
1.
Угол между пересекающимися хордами окружности равен полусумме двух противоположных дуг, высекаемых этими хордами.⇒
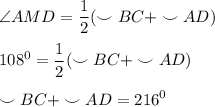 (1)
(1)
Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.⇒
Из (2) выразим дугу AD и подставим в (1):
2. Теперь можем найти искомые углы.
Вписанный угол равен половине градусной меры дуги, на которую он опирается.⇒
∠B = 53°; S=900мм²
Объяснение:
Поперечный разрез паза имеет форму равнобедренной трапеции.
Нам надо найти угол В и площадь данной трапеции.
1. Угол найдем из ΔВАС.
Рассмотрим ΔВАС - прямоугольный.
Высота, опущенная из вершины тупого угла на большее основание, делит его на части, меньшая из которых равна полуразности оснований.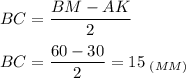
Тангенс угла - отношение противолежащего катета к прилежащему.По таблице найдем угол:
∠В ≈ 53°
2. Найдем площадь трапеции:
Площадь трапеции равна произведению полусуммы оснований на высоту.