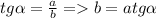надо. Известно, что на плоскости через точку, не принадлежащую данной прямой, проходит единственная прямая, не пересекающаяся данную. Будет ли это утверждение верно для пространства? Можно с объяснением

ответ:  Это любая точка биссектрисы угла, удаленная на заданное расстояние от вершины.

Объяснение:

Что бы построить биссектрису, надо с центром в вершине угла построить окружность, пересекающую стороны угла (у нас это точки В и С).

Далее, с постоянным раствором циркуля, с центрами в точках В и С построить окружности, пересекающиеся в двух точках ( у нас это точки М и Н. Если через них провести прямую АН, то она и будет биссектрисой.

1. Все точки биссектрисы принадлежат углу, так как углом называется вся часть плоскости, ограниченная сторонами угла (то есть все, что находится внутри сторон.

2. Расстояние от точки до прямой - перпендикуляр от точки к этой прямой. Поэтому получившиеся прямоугольные треугольники АКД и АЕД равны по гипотенузе (АД) и острому углу (биссектриса делит угол пополам). А раз так, то КД=ДЕ, то есть точка Д равноудалена от сторона угла.

3. Ну а заданное расстояние это отрезок АД,

Что и требовалось доказать

Объяснение:

Если у прямоугольных треугольников равен острый угол, то это значит, что тангенс этого угла будет одинаковый у обоих треугольников. Тангенс - это отношение противолежащего катета к прилежащему. Значит,

- равный угол, а и b - катеты. Из выражения видим, что если тангенс и один из катетов у треугольников равны, то и второй катет у них тоже будет равным. Если у прямоугольных треуцгольников равны 2 катета, то корень и суммы их квадратов(это их гипотенуза) у них тоже будет равным. Или же они равны по двум катетам и углу между ними.