На рисунке изображен график линейной функции. Напишите формулу, которая задает линейную функцию
. Уравнение прямой в отрезках
Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид где a и b - некоторые отличные от нуля действительные числа , при чем | a| и |b| равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy, считая от начала координат.
. Через координаты 2-х точек.
Уравнение прямой у=кх+в.
Точка пересечения с Оу имеет координаты ( 0; 4)⇒ 4= к*0+в ,в=4
Точка пересечения с Ох имеет координаты (-4; 0) ⇒ 0=к*(-4)+в или
На рисунке изображен график линейной функции. Напишите формулу, которая задает линейную функцию
. Уравнение прямой в отрезках
Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид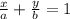
где a и b - некоторые отличные от нуля действительные числа , при чем | a| и |b| равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy, считая от начала координат.
. Через координаты 2-х точек.
Уравнение прямой у=кх+в.
Точка пересечения с Оу имеет координаты ( 0; 4)⇒ 4= к*0+в ,в=4
Точка пересечения с Ох имеет координаты (-4; 0) ⇒ 0=к*(-4)+в или
0=-4к+4 , к=1.
Уравнение прямой у=х+4.
Объяснение:
1)∠АОС-центральный, равен величине дуги, на которую опирается⇒∪АС=130°
∠АВС-вписанный, равен половине величины дуги, на которую опирается ∠АВС=130°:2=65°
2)дуга DAB равна 180°, т.к. DB-диаметр, ∠АОD-центральный⇒∪AD=68°
∪АВ=∪DAB-∪AD=180°-68°=112°
∠АСВ-вписанный, опирается на ∪АВ ∠АСВ=112°:2=56°
3)∪ВАС=180° (ВС-диаметр)
∪АС=2·40°=80° (∠АВС-вписанный, опирается на ∪АС)
∪ВА=∪ВАС-∪АС=180°-80°=100°
4)∠NKL=∠NML=38°(вписанные углы, опираются на одну и туже дугу)
5)∪АС=2·140°=280° (∠АВС-вписанный, опирается на ∪АС)
∪АВС=360°-280°=80° ∠АОС=80° т.к. он центральный и опирается на эту дугу
6)∠ABD-вписанный, опирается на ∪AD⇒ равен половине этой дуги
∪AD=∪ADC-∪DC
∪ADC=2·56° (на неё опирается вписанный ∠АВС)
∪DC=2·42° (на неё опирается вписанный ∠DAC)
∪AD=2·56°-2·42°=2(56°-42°)
∠ABD=2(56°-42°)/2=14°