Нарисуйте в тетради куб, обозначьте нижнее основание ABCD, а верхнее A₁B₁C₁D₁.
ответьте на во Написать все прямые, принадлежащие плоскости АА₁D₁D.
2. Написать все прямые, параллельные A₁B₁.
3. Написать все прямые, параллельные плоскости AA₁D₁D.
4. Написать все прямые, скрещивающиеся с прямой A₁D.
5. Написать все прямые, перпендикулярные СС₁ и пересекающиеся с ней.
6. Написать все прямые, перпендикулярные плоскости AA₁D₁D.
7. Указать проекцию для прямой А₁D на плоскость ABCD.
8. Указать угол, который образует прямая А₁В с плоскостью АА₁D₁D.
9. Указать угол, который образует прямая BD₁ с плоскостью ABCD.
10. Указать ребро двугранного угла, образованного плоскостями АВ₁С₁D и ABCD.
11. Указать ребро двугранного угла, образованного плоскостями ВDС₁ и ABCD.
12. Доказать что прямая АD₁ и ВВ₁ скрещиваются.
13. Доказать, что прямая A₁B₁ параллельна плоскости ABCD.
14. Доказать, что прямая A₁B₁ перпендикулярна плоскости AA₁D₁D.
15. Доказать, что плоскости AA₁D₁D и BB₁C₁C параллельны.
16. Доказать, что плоскости AA₁В₁В и AA₁D₁D перпендикулярны.
В ромбе диагонали точкой пересечения делятся пополам (АО=ОС и ВО=OD).
Пусть ВО=х, тогда:
AC-BD=14
AC-2x=14
AC=14+2x
2·OC=2(x+7)
OC=x+7
Из ΔBCO по т. Пифагора:
x=-15 не подходит по смыслу задачи, поэтому один корень х=8.
ВО=х=8 см
ОС=х+7=8+7=15 см
АС=АО+ОС=15+15=30 см
BD=BO+OD=8+8=16 см
Вспомним такую формулу: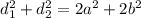 , где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).
, где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).
Найдем диагонали, составив систему:
Пусть АС=х, BD=y.
Отрицательные значения нам не подходят, так как длинна - величина неотрицательная.
Тогда AC=x=30см, BD=y=16см.
ответ: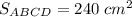
Объяснение:
d₁-d₂=14
d₁=14+d₂
Діагоналі у точці перетину діляться навпіл і утворюють прямокутні трикутники.Катети дорівнюють половинам діагоналей: 14+d₂ / 2 та d₂/2.
За теоремою Піфагора:
17²=(14+d₂ /2)²+ (d₂/2)²
289=(14+d₂)² /4+d₂²/4
289*4=(14+d₂)² +d₂²
1156=14²+28d₂+d₂²+d₂²
2d₂²+28d₂-960=0 :2
d₂²+14d₂-480=0
D = b² - 4ac = 14² - 4·1·(-480) = 196 + 1920 = 2116
x₁ = -14 - √2116 /2·1 = -14 - 46/ 2 = -60 /2 = -30 не підходить
x₂ = -14 + √2116/ 2·1 = -14 + 46 /2 = 32/ 2 = 16 см -d₂
d₁=16+14 = 30 см
S=1/2× 16×30=240 см²