***
∠ОАВ = ∠OCD
как накрест лежащие углы,
( накрест лежащие углы _ это углы, которые лежат во внутренней области по разные стороны от секущей - накрест друг от друга )
при пересечении параллельных прямых АВ и CD секущей АС
∠АОВ = ∠COD как вертикальные углы
( вертикальные углы _ пара углов, у которых вершина общая, а стороны одного угла составляют продолжение сторон другого угла )
если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
⇔
ΔOAB ~ ΔOCD по двум углам
OD = BD - OB = 8 - 4 = 4 см
получаем:
ОА / ОС = OB / OD
⇒
3 / OC = 4 / 4
отсюда находим ОС умножая крест накрест
OC = (4 · 3) / 4 = 3 см = OA
=>
AC = OA + OC = 3+3 = 6 см
ответ: 6 см
8. x=27, y=21, z= 24
7. = 50
4. x=44 y=33 z=22
Объяснение:
8. Так как треугольники подобны, то и отношение между сторонами такие же как и в первом треугольнике x~RK, z~RT
x+z=51
RK+RT=17
k=51/17, т.е. во сколько раз R1K1T1 больше RKT
следовательно x=9*3=27, y=7*3=21, z=8*3= 24
7. Опять из подобия треугольников делаем вывод что к=5 (25/5) следовательно и площадь = 5*10=50
4. Отношения сторон равны 4 : 3 : 2 в сумме дают 9, так как периметр равен 99, то одна часть стороны равна 11 следовательно
x=4*11=44, y=3*11=33, z=2*11=22
***
∠ОАВ = ∠OCD
как накрест лежащие углы,
( накрест лежащие углы _ это углы, которые лежат во внутренней области по разные стороны от секущей - накрест друг от друга )
при пересечении параллельных прямых АВ и CD секущей АС
∠АОВ = ∠COD как вертикальные углы
( вертикальные углы _ пара углов, у которых вершина общая, а стороны одного угла составляют продолжение сторон другого угла )
если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
⇔
ΔOAB ~ ΔOCD по двум углам
OD = BD - OB = 8 - 4 = 4 см
получаем:
ОА / ОС = OB / OD
⇒
3 / OC = 4 / 4
отсюда находим ОС умножая крест накрест
OC = (4 · 3) / 4 = 3 см = OA
=>
AC = OA + OC = 3+3 = 6 см
ответ: 6 см
8. x=27, y=21, z= 24
7.
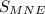= 50
4. x=44 y=33 z=22
Объяснение:
8. Так как треугольники подобны, то и отношение между сторонами такие же как и в первом треугольнике x~RK, z~RT
x+z=51
RK+RT=17
k=51/17, т.е. во сколько раз R1K1T1 больше RKT
следовательно x=9*3=27, y=7*3=21, z=8*3= 24
7. Опять из подобия треугольников делаем вывод что к=5 (25/5) следовательно и площадь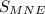
= 5*10=50
4. Отношения сторон равны 4 : 3 : 2 в сумме дают 9, так как периметр равен 99, то одна часть стороны равна 11 следовательно
x=4*11=44, y=3*11=33, z=2*11=22