По ф.Герона: S=√[p(p-a)(p-b)(p-c)], где р - полупериметр треугольника, a, b и с - его стороны. р-(37+37+24):2=49 S=√[49•12•12•25]=7•12•5=420 (ед. площади)
Опустим высоту на основание. Высота равнобедренного треугольника, проведенная между равными сторонами, делит его на два равных прямоугольных, в которых боковые стороны треугольника - гипотенузы, высота и половина основания - катеты. . Тогда по т.Пифагора h=√(37²-(24/2)²)=35 S=h•a/2=35•24/2=420 (ед. площади).
Найдите диаметр круга, если хорда длиной 2V6 см перпендикулярна диаметру и делит его на отрезки в отношении 2:3.
Объяснение:
ΔОМА=ΔОМВ как прямоугольные по двум катетам ОМ-общий, ОА=ОВ как катеты ⇒МА=МВ=2√6:2=√6 (см)
По т. об отрезках пересекающихся хорд АМ*МВ=СМ*МД
Т.к. СМ/МД=2/3 , то МД=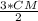
. Получим √6*√6= СМ* 
.
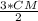СМ²=4, СМ=2 см .
Тогда МД=3 см , поэтому диаметр равен d= СМ+МД=2+3=5 (см).
d=5 см
=====================
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
По ф.Герона:
S=√[p(p-a)(p-b)(p-c)], где р - полупериметр треугольника, a, b и с - его стороны.
р-(37+37+24):2=49
S=√[49•12•12•25]=7•12•5=420 (ед. площади)
Опустим высоту на основание. Высота равнобедренного треугольника, проведенная между равными сторонами, делит его на два равных прямоугольных, в которых боковые стороны треугольника - гипотенузы, высота и половина основания - катеты. .
Тогда по т.Пифагора
h=√(37²-(24/2)²)=35
S=h•a/2=35•24/2=420 (ед. площади).