Очевидно, этот угол равен 30 градусам. Длина хорды равна радиусу. Треугольник с вершинами : центр окружности , концы хорды -равносторонний. Одна из его сторон перпендикулярна касательной. Отсюда ответ: 90-60=30.
Пользуясь рисунком, (см. вложение) и зная, что — диаметр окружности, — хорда окружности, определим .
В окружности половиной диаметра являются радиусы, значит, эти радиусы будут равны и хорде:
В образовавшемся треугольнике получается, что все три стороны по длине равны, следовательно, этот треугольник является равносторонним, у которого все углы равны по .
Как известно, точка касания касательной к окружности и радиуса окружности пересекаются под прямым углом ().
Отсюда следует, чтобы узнать , нужно найти разность развёрнутого угла () от суммы других известных углов:
Очевидно, этот угол равен 30 градусам. Длина хорды равна радиусу. Треугольник с вершинами : центр окружности , концы хорды -равносторонний. Одна из его сторон перпендикулярна касательной. Отсюда ответ: 90-60=30.
Пользуясь рисунком, (см. вложение) и зная, что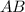 — диаметр окружности,
— диаметр окружности, 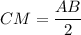 — хорда окружности, определим
— хорда окружности, определим 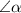 .
.
В окружности половиной диаметра являются радиусы, значит, эти радиусы будут равны и хорде: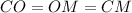
В образовавшемся треугольнике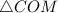 получается, что все три стороны по длине равны, следовательно, этот треугольник является равносторонним, у которого все углы равны по
получается, что все три стороны по длине равны, следовательно, этот треугольник является равносторонним, у которого все углы равны по 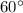 .
.
Как известно, точка касания касательной к окружности и радиуса окружности пересекаются под прямым углом (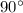 ).
).
Отсюда следует, чтобы узнать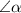 , нужно найти разность развёрнутого угла (
, нужно найти разность развёрнутого угла (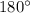 ) от суммы других известных углов:
) от суммы других известных углов:
ответ: 30°