Для начала, нужно выделить две формулы, по которым мы будем находить P и S трапеции.
Для нахождения P трапеции, нам всего лишь нужно сложить все стороны и посчитать.
Для нахождения S трапеции, есть формула (a+b)/2 * h.
Ищем периметр:
1. AB = CD= 4 см ( т.к. углы А и D равны, следовательно стороны при основании будут равны ).
2. Проведём два перпендикуляра из точек B и C. У нас получатся два прямоугольных треугольника и прямоугольник ( еще не доказано )
3. ∠ABK = 90 - 60 = 30° ( т.к. ∠А уже равен 90°) ⇒ AK = 4:2 = 2 см ( т.к. катет, лежащий напротив угла в 30° будет равен половине гипотенузы ).
4. Треугольник ABK и HCD равны по катету и углу ( AB=CD, ∠A=∠D ) ⇒ AK=HD=2 см.
5. Четырёхугольник KBCH - прямоугольником ( ∠K = ∠B и ∠H = ∠C, т.к. являются односторонними углами, следовательно в сумме они будут получать 180°, а 180-90=90 ) ⇒ BC = KH и BK = CH.
KB⊥BC, AD||BC => KB⊥AD, ∠BKD=90 BO=OD (диагонали параллелограмма точкой пересечения делятся пополам) KO=OD (медиана, проведенная из вершины прямого угла, равна половине гипотенузы)
∠BEK=∠EKD, ∠EBD=∠BDK (накрест лежащие углы при AD||BC) △BOE~△KOD (по двум углам) BO/OD=OE/KO => BO=OE.
ИЛИ Средняя линия параллелограмма (и лежащая на ней точка пересечения диагоналей) делит всякий отрезок, соединяющий противоположные стороны, пополам (по теореме Фалеса). Диагонали четырехугольника BEDK делятся точкой пересечения пополам => BEDK - параллелограмм. В параллелограмме BEDK угол KBE - прямой => BEDK - прямоугольник. Диагонали прямоугольника равны => равны их половины, BO=OE.
P = 18 см, S = 10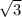 см²
см²
Объяснение:
Для начала, нужно выделить две формулы, по которым мы будем находить P и S трапеции.
Для нахождения P трапеции, нам всего лишь нужно сложить все стороны и посчитать.
Для нахождения S трапеции, есть формула (a+b)/2 * h.
Ищем периметр:
1. AB = CD= 4 см ( т.к. углы А и D равны, следовательно стороны при основании будут равны ).
2. Проведём два перпендикуляра из точек B и C. У нас получатся два прямоугольных треугольника и прямоугольник ( еще не доказано )
3. ∠ABK = 90 - 60 = 30° ( т.к. ∠А уже равен 90°) ⇒ AK = 4:2 = 2 см ( т.к. катет, лежащий напротив угла в 30° будет равен половине гипотенузы ).
4. Треугольник ABK и HCD равны по катету и углу ( AB=CD, ∠A=∠D ) ⇒ AK=HD=2 см.
5. Четырёхугольник KBCH - прямоугольником ( ∠K = ∠B и ∠H = ∠C, т.к. являются односторонними углами, следовательно в сумме они будут получать 180°, а 180-90=90 ) ⇒ BC = KH и BK = CH.
6. AD = AK + HD + KH = 2+2+3 = 7 см.
6. P трапеции = BC + 2CD + AD = 3+4*2+7 = 18 см.
Ищем площадь:
S =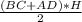
Нужно найти высоту:
1. По теореме пифагора:
BK² = AB² - AK²
BK² = 4² - 2²
BK² = 12
BK =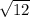 = 2
= 2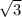 см
см
2. S =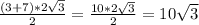 см²
см²
BO=OD (диагонали параллелограмма точкой пересечения делятся пополам)
KO=OD (медиана, проведенная из вершины прямого угла, равна половине гипотенузы)
∠BEK=∠EKD, ∠EBD=∠BDK (накрест лежащие углы при AD||BC)
△BOE~△KOD (по двум углам)
BO/OD=OE/KO => BO=OE.
ИЛИ
Средняя линия параллелограмма (и лежащая на ней точка пересечения диагоналей) делит всякий отрезок, соединяющий противоположные стороны, пополам (по теореме Фалеса). Диагонали четырехугольника BEDK делятся точкой пересечения пополам => BEDK - параллелограмм. В параллелограмме BEDK угол KBE - прямой => BEDK - прямоугольник. Диагонали прямоугольника равны => равны их половины, BO=OE.