Обратим внимание на то, что речь идет о противоположных углах, а не об углах, прилежащих к одной боковой стороне трапеции. Основания трапеции параллельны, каждая боковая сторона при них - секущая. Поэтому сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°, так как они внутренние односторонние при пересечении параллельных прямых секущей.
Обозначим трапецию АВСД. По условию ∠А:∠С=1:2
∠Д:∠В=7:8
Примем угол А=а, тогда угол С=2а.
Примем угол Д=7b, тогда угол В=8b
a+8b=180°
2a+7b=180°
Приравняем левые части уравнений:
а+8b=2a+7b⇒
b=a
Подставим в первое уравнение вместо b – а, т.к. они равны.
Если вас еще интересует решение этой задачи, то здесь не так уж и сложно.
Нужно воспользоваться формулами для нахождения диагоналей параллелограмма через его стороны.
D - большая диагональ, d - малая диагональ.
Подставляем длины сторон и диагоналей и находим угол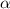
Как видим, углов между сторонами 5 и 3, при которых одна из диагоналей могла бы равняться 8, и при которых сещуствовал бы параллелограмм, нет.
Вот и вывод: диагональ параллелограмма не может равняться 8 при сторонах 5 и 3.
Обратим внимание на то, что речь идет о противоположных углах, а не об углах, прилежащих к одной боковой стороне трапеции. Основания трапеции параллельны, каждая боковая сторона при них - секущая. Поэтому сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°, так как они внутренние односторонние при пересечении параллельных прямых секущей.
Обозначим трапецию АВСД. По условию ∠А:∠С=1:2
∠Д:∠В=7:8
Примем угол А=а, тогда угол С=2а.
Примем угол Д=7b, тогда угол В=8b
a+8b=180°
2a+7b=180°
Приравняем левые части уравнений:
а+8b=2a+7b⇒
b=a
Подставим в первое уравнение вместо b – а, т.к. они равны.
Тогда а+8а=180°⇒
а=20° и b=20°.
Следовательно, ∠ВАД=20°, ∠АВС=8•20°=160°;
∠ВСД=2•20=40°; ∠СДА=7•20=140°.