Образующая усеченного конуса наклонена к плоскости большего основания под уголком 30градусов. Радиусы оснований равны 6 и 3 см. Найти площадь полной поверхности усечённого конуса
В прямоугольной трапеции ABCD с основаниями BC и AD и высотой AB диагонали AC и BD перпендикулярны друг другу . Известно отношение оснований BC : AD = m : n . Найдите отношение длин диагоналей AC : BD.
Пусть BC = mx и AD = nx. Из вершины С проведём прямую параллельной диагонали BD до пересечения прямой на продолжении основания AD, AC ⊥ CE.
Из вершины угла С проведем высоту CF.
Из прямоугольного треугольника ACE, каждый катет есть среднее пропорциональное между проекцией катета и гипотенузой:
В трапеции пересечение продолжений боковых сторон и середины оснований лежат на одной прямой. О - середина EF.
EO=OF=3, EF=6
Биссектриса внутреннего угла при параллельных отсекает равнобедренный треугольник (∠EOB=∠CBO, накрест лежащие. ∠EOB=∠EBO).
BE=EO=3, AE=18
△ABC~△AEF (по соответственным углам при BC||EF)
BC/EF=AB/AE =21/18 =7/6, BC=7
AC=√(21^2 -7^2) =√(14*28) =14√2
Точка О лежит на биссектрисе угла ABC, следовательно равноудалена от сторон угла. Расстояние между параллельными постоянно, поэтому достаточно найти FC.
В прямоугольной трапеции ABCD с основаниями BC и AD и высотой AB диагонали AC и BD перпендикулярны друг другу . Известно отношение оснований BC : AD = m : n . Найдите отношение длин диагоналей AC : BD.
Пусть BC = mx и AD = nx. Из вершины С проведём прямую параллельной диагонали BD до пересечения прямой на продолжении основания AD, AC ⊥ CE.
Из вершины угла С проведем высоту CF.
Из прямоугольного треугольника ACE, каждый катет есть среднее пропорциональное между проекцией катета и гипотенузой:
Следовательно,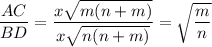
Через точку O проведем EF||BC.
В трапеции пересечение продолжений боковых сторон и середины оснований лежат на одной прямой. О - середина EF.
EO=OF=3, EF=6
Биссектриса внутреннего угла при параллельных отсекает равнобедренный треугольник (∠EOB=∠CBO, накрест лежащие. ∠EOB=∠EBO).
BE=EO=3, AE=18
△ABC~△AEF (по соответственным углам при BC||EF)
BC/EF=AB/AE =21/18 =7/6, BC=7
AC=√(21^2 -7^2) =√(14*28) =14√2
Точка О лежит на биссектрисе угла ABC, следовательно равноудалена от сторон угла. Расстояние между параллельными постоянно, поэтому достаточно найти FC.
AF/AC =6/7 => FC=AC-AF =AC/7 =2√2