Чтобы найти расстояние d от пункта A до недоступного пункта C, на местности выбрали точку B и измерили длину с отрезка AB и углы α и β. Найдите расстояние от пункта A до пункта C, если AB = 30 м, α = 60°, β = 45°
————
Сделав рисунок по условию задачи, получим треугольник АВС с основанием АВ и углами ∠САВ=60° и ∠СВА=45°.
Из суммы углов треугольника ∠АСВ=180°-(45°+60°)=75°
По т.синусов АВ:sin75°=AC:sin45°.
Табличное значение sin75°= (√3+1)/2√2; sin45°=√/2 ⇒
21, 96 м.
Объяснение:
Чтобы найти расстояние d от пункта A до недоступного пункта C, на местности выбрали точку B и измерили длину с отрезка AB и углы α и β. Найдите расстояние от пункта A до пункта C, если AB = 30 м, α = 60°, β = 45°
————
Сделав рисунок по условию задачи, получим треугольник АВС с основанием АВ и углами ∠САВ=60° и ∠СВА=45°.
Из суммы углов треугольника ∠АСВ=180°-(45°+60°)=75°
По т.синусов АВ:sin75°=AC:sin45°.
Табличное значение sin75°= (√3+1)/2√2; sin45°=√/2 ⇒
30•2√2:(√3+1)=d:(√2/2) ⇒
AС=d= 60/(√3+1) или ≈ 21,96 м.
1) ∡МНО = 45
2)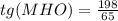
Объяснение:
Рассчитайте величину двугранного угла при основании правильной четырехугольной пирамиды если:
1.сторона основания равна 3,6 м, а высота равна 1,8 м
(ABCD-квадрат) а = 3,6
ΔMOH OH = 0.5a=1.8; OM ⊥ OH; MO= 1,8 ⇒ ΔMOH прямоугольный равнобедренный ОМ = ОН = 1,8; ∡МОН = 90° ⇒ ∡МНО = 45
2.сторона основания равна 65 см, а высота равна 99 см
(ABCD-квадрат) а = 65
ΔMOH OH = 0.5a=65/2 OM ⊥ OH; MO= 99 ⇒ ΔMOH прямоугольный ∡МОН = 90° ⇒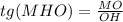
известен тангенс угла, а следовательно и сам угол при необходимости можно найти по таблицам Брадиса