1) Проведём две высоты к плоскости ABCD из вершин и И отметим их как и соответственно.
2)Рассмотрим полученный треугольник ; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна , то можно и найти
(Против угла в 30 градусов лежит катет равный половине гипотенузы).
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника:
5)Следует детально рассмотреть треугольник В нем известны две стороны, и он прямоугольный, а значит можно найти по теореме Пифагора. .
6)Отсюда можно найти .
. Знаю эту величину можем найти искомую АB.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат. ; Но также стоит заметить, что , но второй намного легче, чем мучиться с преобразованием корневых выражений.
Задание 1. Доказать, что диагонали делят параллелограмм на 4 равновеликих треугольника. Доказательство. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть половина первой диагонали = а, а половина второй диагонали = b. Значит площадь каждого из получившихся треугольников равна (1/2)a*b*Sinα - формула, где α - угол между диагоналями. Углы, образованные при пересечении диагоналей - смежные и равны α и 180-α. Поскольку Sin(180-α) = Sinα (формула), то площади всех 4 треугольников равны. Что и требовалось доказать. Задание 2. Найти площадь равнобокой трапеции с основаниями 15 см и 39 см, в которой диагональ перпендикулярна к боковой стороне. Решение. Поскольку высота из тупого угла равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности оснований = 12см (свойство), а высота нашей трапеции - высота прямоугольного треугольника из прямого угла, то эта высота по ее свойствам равна h=√((39-12)*12)=18см. Тогда площадь трапеции равна по формуле S=(AD+BC)*h/2 : S=(39+15)*18/2=486см². Задание 3. Соответствующие стороны двух подобных треугольников относятся как 2 : 3. Площадь второго треугольника равна 81 см2. Найдите площадь первого треугольника. Площади подобных треугольников относятся как квадрат коэффициента подобия. Значит S1=(2/3)²*S2. S1=(4/9)*81=36см². Задание 4. Основания трапеции относятся как 2:3, а ее площадь равна 50 см2. Найти площади: а) двух треугольников, на которые данная трапеция делится диагональю б) четырех треугольников, на которые данная трапеция делится диагоналями. Решение. Диагонали трапеции делят ее на 4 треугольника, из которых два, прилежащих к основаниям, подобны, а два прилежащих к боковым сторонам, равновелики (равны по площади). а). Sabcd=(2x+3x)*h/2 =50см² (площадь трапеции дана). => 5xh=100см² и xh=20см². Sabd=Sacd=(1/2)*3xh = 30см². Sabo=Scod= Sabcd-Sabd= 50-30=20см². ответ: 30см² и 20см². б) Sboc=(1/2)*2x*(2/5)h=0,4*xh =0,4*20=8см². Saod=(1/2)*3x*(3/5)h=0,9*xh =0,9*20=18см². Saob=Saod=Sabd-Scod=(1/2)*3xh - 0,9*xh = 06xh =12см². ответ: Sboc=8см²,Saod=18см², Saob=Saod=12см².
Дано:
Найти: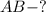
1) Проведём две высоты к плоскости ABCD из вершин и
и 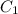 И отметим их как
И отметим их как 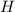 и
и 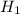 соответственно.
соответственно.
2)Рассмотрим полученный треугольник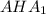 ; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна
; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна 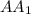 , то можно и найти
, то можно и найти 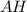
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем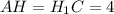
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника: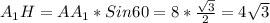
5)Следует детально рассмотреть треугольник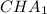 В нем известны две стороны, и он прямоугольный, а значит можно найти
В нем известны две стороны, и он прямоугольный, а значит можно найти 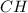 по теореме Пифагора.
по теореме Пифагора. 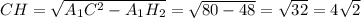 .
.
6)Отсюда можно найти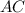 .
.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат.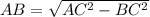 ; Но также стоит заметить, что
; Но также стоит заметить, что 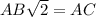 , но второй намного легче, чем мучиться с преобразованием корневых выражений.
, но второй намного легче, чем мучиться с преобразованием корневых выражений. 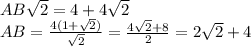
ответ: AB= двум корней из двух плюс 4
Доказать, что диагонали делят параллелограмм на 4 равновеликих треугольника.
Доказательство.
Диагонали параллелограмма точкой пересечения делятся пополам.
Пусть половина первой диагонали = а, а половина второй диагонали = b.
Значит площадь каждого из получившихся треугольников равна
(1/2)a*b*Sinα - формула, где α - угол между диагоналями.
Углы, образованные при пересечении диагоналей - смежные и равны
α и 180-α.
Поскольку Sin(180-α) = Sinα (формула), то площади всех 4 треугольников равны.
Что и требовалось доказать.
Задание 2.
Найти площадь равнобокой трапеции с основаниями 15 см и 39 см, в которой диагональ перпендикулярна к боковой стороне.
Решение.
Поскольку высота из тупого угла равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности оснований = 12см (свойство), а высота нашей трапеции - высота прямоугольного треугольника из прямого угла, то эта высота по ее свойствам равна
h=√((39-12)*12)=18см. Тогда площадь трапеции равна по формуле
S=(AD+BC)*h/2 :
S=(39+15)*18/2=486см².
Задание 3.
Соответствующие стороны двух подобных треугольников относятся как 2 : 3. Площадь второго треугольника равна 81 см2. Найдите площадь первого треугольника.
Площади подобных треугольников относятся как квадрат коэффициента подобия. Значит S1=(2/3)²*S2.
S1=(4/9)*81=36см².
Задание 4.
Основания трапеции относятся как 2:3, а ее площадь равна 50 см2. Найти площади:
а) двух треугольников, на которые данная трапеция делится диагональю
б) четырех треугольников, на которые данная трапеция делится диагоналями.
Решение.
Диагонали трапеции делят ее на 4 треугольника, из которых два, прилежащих к основаниям, подобны, а два прилежащих к боковым сторонам, равновелики (равны по площади).
а). Sabcd=(2x+3x)*h/2 =50см² (площадь трапеции дана). =>
5xh=100см² и xh=20см².
Sabd=Sacd=(1/2)*3xh = 30см².
Sabo=Scod= Sabcd-Sabd= 50-30=20см².
ответ: 30см² и 20см².
б) Sboc=(1/2)*2x*(2/5)h=0,4*xh =0,4*20=8см².
Saod=(1/2)*3x*(3/5)h=0,9*xh =0,9*20=18см².
Saob=Saod=Sabd-Scod=(1/2)*3xh - 0,9*xh = 06xh =12см².
ответ: Sboc=8см²,Saod=18см², Saob=Saod=12см².