Основание пирамиды - равнобедренный треугольник с основанием 6 см и высотой 9 см. Каждое из боковых ребер пирамиды имеет длину 13 см. Найти высоту пирамиды.

Показать ответ

Ответ:

necoshevcom

29.07.2020 22:23

Так как четырехугольник ABCD вписан в окружность, а диагонали AC и BC перпендикулярны, то эти диагонали делят заданный четырёхугольник на 4 прямоугольных треугольника.
Эти треугольники попарно подобны (по вертикальным углам при пересечении диагоналей) по равенству двух вписанных углов, опирающихся на равные дуги.

Обозначим точку пересечения диагоналей Е, центр описанной около четырёхугольника окружности О.

Из подобия треугольников АВЕ и ДЕС следует АЕ:ЕД = 3:4.
Примем коэффициент подобия у.
Тогда 8² = (3у)² + (4у)²,
9у² + 16у² = 64,
25у² = 64,
у = √(64/25) = 8/5.
Получаем: АЕ = 3х = 24/5 = 4,8.
ДЕ = 4х = 32/5 = 6,4.

Угол АВД как вписанный равен (1/2) центрального угла АОД.
Синус (1/2) центрального угла АОД равен (8/2)/(17/2) = 4/8,5 = 0,470588. Угол АBД равен 0,489957 радиан или 28,07249°.
Косинус угла ЕАД = 4,8/8 = 0,6.
Угол ЕАД = 0,927295 радиан или 53,1301°.
Угол АДЕ = 90° - 53,1301 = 36,8699°.
По теореме синусов находим АB = AD*sin АДЕ / sin АBД =
= 8*0,6/ 0.470588 = 10,2.

Сторона ДС по заданию равна (4/3) АВ = (4/3)*10,2 = 13,6.

ВЕ = √10,2²-4,8²) = √( 104.04 - 23.04) = √81 = 9.
СЕ = √(13,6²-6,4²) = √( 184.96 - 40.96) = √144 = 12.
ВС = √(9²+12²) = √(81+144) = √= 15.

0,0(0 оценок)

Ответ:

таня43564

04.01.2021 23:10

1. Угол между боковым ребром и плоскостью основания пирамиды равен 45°.

2. Объем пирамиды равен 24 ед.³

Объяснение:

Требуется найти:

1. Угол между боковым ребром и плоскостью основания пирамиды.

2. Объем пирамиды.

476.

Дано: SABCD - правильная пирамида.

∠DSC - 60°;

Найти: ∠SCO.

В основании правильной четырехугольной пирамиды лежит квадрат, а боковые грани - равнобедренные треугольники.

1. Рассмотрим ΔDSC - равнобедренный.

Углы при основании равнобедренного треугольника равны.

∠DSC = 60° ⇒ ∠SDC = ∠SCD = (180° - 60°) : 2 = 60°

⇒ ΔDSC - равносторонний.

⇒ Все ребра пирамиды равны.

Пусть ребро пирамиды равно а.

2. Рассмотрим ΔАСD - прямоугольный.

По теореме Пифагора:

AC² = AD² + DC²

AC = a√2

Диагонали квадрата точкой пересечения делятся пополам.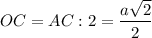

⇒ $\displaystyle OC=AC:2=\frac{a\sqrt{2} }{2}$

3. Рассмотрим ΔОSC - прямоугольный.

Пусть ∠SCO = α

Косинус угла равен отношению прилежащего катета к гипотенузе.

$\displaystyle cos\;\alpha =\frac{OC}{SC} =\frac{a\sqrt{2} }{2\cdot {a}} =\frac{\sqrt{2} }{2}$

⇒ α = 45°

Угол SCO равен 45°.

486.

Дано: SABC - пирамида;

ВС = 9; АС = 10; АВ = 17;

Грани составляют с плоскостью основания углы в 45°.

Найти: V пирамиды.

Если боковые грани пирамиды наклонены к плоскости основания под одинаковым углом, то высота, опущенная из вершины на основание, падает в центр вписанной в основание окружности.

Объем пирамиды равен:

$\displaystyle \boxed { V=\frac{1}{3}Sh }$ , где S - площадь основания, h - высота пирамиды.

1. Радиус вписанной окружности найдем по формуле:

$\displaystyle \boxed {S=pr} \Rightarrow \boxed{r=\frac{S}{p} }$ ,

где S - площадь треугольника, р - полупериметр.

p = (9 + 10 + 17) : 2 = 18 (ед.)

Площадь найдем по формуле Герона:

$S=\sqrt{p(p-a)(p-b)(p-c)}$ , где a, b, c - стороны треугольника.

$\displaystyle S=\sqrt{18(18-9)(18-10)(18-17}=\sqrt{18\cdot9\cdot8\cdot1}=36$ (ед.²)

Тогда радиус равен:

r = ОН = 36 : 18 = 2 (ед.)

2. Рассмотрим ΔОSH - прямоугольный.

Угол между боковой гранью и основанием равен двугранному углу SBCO.Двугранный угол измеряется величиной линейного угла, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.

⇒∠SHO = 45°

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠HSO = 90° - 45° = 45°

Тогда ΔОSH - равнобедренный.

⇒ ОН = SO = 2 (ед.)

3. Найдем объем:

$\displaystyle V=\frac{1}{3}\cdot36 \cdot2=24$ (ед.³)