Основанием прямого параллелепипеда abcda1b1c1d1 является ромб авсd, сторона которого равна 6 см и угол равен . плоскость аd1c1 составляет с плоскостью основания угол. найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда.

Показать ответ

Ответ:

таня43564

04.01.2021 23:10

1. Угол между боковым ребром и плоскостью основания пирамиды равен 45°.

2. Объем пирамиды равен 24 ед.³

Объяснение:

Требуется найти:

1. Угол между боковым ребром и плоскостью основания пирамиды.

2. Объем пирамиды.

476.

Дано: SABCD - правильная пирамида.

∠DSC - 60°;

Найти: ∠SCO.

В основании правильной четырехугольной пирамиды лежит квадрат, а боковые грани - равнобедренные треугольники.

1. Рассмотрим ΔDSC - равнобедренный.

Углы при основании равнобедренного треугольника равны.

∠DSC = 60° ⇒ ∠SDC = ∠SCD = (180° - 60°) : 2 = 60°

⇒ ΔDSC - равносторонний.

⇒ Все ребра пирамиды равны.

Пусть ребро пирамиды равно а.

2. Рассмотрим ΔАСD - прямоугольный.

По теореме Пифагора:

AC² = AD² + DC²

AC = a√2

Диагонали квадрата точкой пересечения делятся пополам.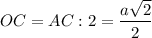

⇒ $\displaystyle OC=AC:2=\frac{a\sqrt{2} }{2}$

3. Рассмотрим ΔОSC - прямоугольный.

Пусть ∠SCO = α

Косинус угла равен отношению прилежащего катета к гипотенузе.

$\displaystyle cos\;\alpha =\frac{OC}{SC} =\frac{a\sqrt{2} }{2\cdot {a}} =\frac{\sqrt{2} }{2}$

⇒ α = 45°

Угол SCO равен 45°.

486.

Дано: SABC - пирамида;

ВС = 9; АС = 10; АВ = 17;

Грани составляют с плоскостью основания углы в 45°.

Найти: V пирамиды.

Если боковые грани пирамиды наклонены к плоскости основания под одинаковым углом, то высота, опущенная из вершины на основание, падает в центр вписанной в основание окружности.

Объем пирамиды равен:

$\displaystyle \boxed { V=\frac{1}{3}Sh }$ , где S - площадь основания, h - высота пирамиды.

1. Радиус вписанной окружности найдем по формуле:

$\displaystyle \boxed {S=pr} \Rightarrow \boxed{r=\frac{S}{p} }$ ,

где S - площадь треугольника, р - полупериметр.

p = (9 + 10 + 17) : 2 = 18 (ед.)

Площадь найдем по формуле Герона:

$S=\sqrt{p(p-a)(p-b)(p-c)}$ , где a, b, c - стороны треугольника.

$\displaystyle S=\sqrt{18(18-9)(18-10)(18-17}=\sqrt{18\cdot9\cdot8\cdot1}=36$ (ед.²)

Тогда радиус равен:

r = ОН = 36 : 18 = 2 (ед.)

2. Рассмотрим ΔОSH - прямоугольный.

Угол между боковой гранью и основанием равен двугранному углу SBCO.Двугранный угол измеряется величиной линейного угла, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.

⇒∠SHO = 45°

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠HSO = 90° - 45° = 45°

Тогда ΔОSH - равнобедренный.

⇒ ОН = SO = 2 (ед.)

3. Найдем объем:

$\displaystyle V=\frac{1}{3}\cdot36 \cdot2=24$ (ед.³)