Основой пирамиды MABCD является прямоугольник ABCD, AC=16cm, угол CAD = 30cm, найти модуль вектора b = MB - MD - DA

Показать ответ

Ответ:

ariannaajoseph9

04.06.2020 13:59

KK₁ = 3 ед.

Объяснение:

Дано: прямая АВ;

АК=КВ;

АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ.

АА₁ = 5; ВВ₁ = 11.

Найти: КК₁

Пусть А₁В₁= 2а.

Если две прямые перпендикулярны третьей, то они параллельны между собой.

АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ ⇒ АА₁ || ВВ₁ || КК₁.

Теорема Фалеса:

Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

АК = КВ ⇒ А₁К₁ = К₁В₁ = а.

Рассмотрим ΔА₁АО и ΔОВВ₁ - прямоугольные.

Вертикальные угла равны.

∠1 = ∠2 (вертикальные)

⇒ ΔА₁АО ~ ΔОВВ₁ (по двум углам)

Составим пропорцию:

$\displaystyle \frac{A_1O}{OB_1}=\frac{A_1A}{B_1B} \frac{A_1O}{OB_1}=\frac{5}{11}$

Пусть А₁О = 5х, тогда ОВ₁ = 11х

Составим уравнение:

$\displaystyle 5x+11x=2a\\16x=2a\\x=\frac{a}{8}$

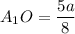
⇒ $\displaystyle A_1O=\frac{5a}{8}$

Тогда

$\displaystyle OK_1=a-\frac{5a}{8}=\frac{3a}{8}$

Рассмотрим ΔА₁АО и ΔК₁КО - прямоугольные.

∠1=∠2 (вертикальные)

⇒ ΔА₁АО ~ ΔК₁КО

Составим пропорцию:

$\displaystyle \frac{AA_1}{KK_1}=\frac{A_1O}{OK_1} frac{5}{KK_1}=\frac{5a*8}{8*3a} =\frac{5}{3}KK_1=\frac{5*3}{5}=3$

Точки A и B лежат в разных полуплоскостях относительно прямойA1B1 .Отрезки AA1 и BB1 перепендикулярн

0,0(0 оценок)

Ответ:

Одуванчик11111111

29.02.2020 11:32

$\displaystyle OM=\frac{a}{4}$

Объяснение:

Дано: ΔАВС;

АК и СЕ - медианы;

СМ = МЕ; АО = ОК;

АС = а

Найти: ОМ.

1. СМ = МЕ; АО = ОК

Обратная теорема Фалеса: Если две или более прямых отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные. Утверждение справедливо, независимо от того, параллельные прямые или пересекаются.

⇒ ЕК || ОМ || АС

2. Рассмотрим АВС.

АЕ = ЕВ; СК = КВ (АК и СЕ - медианы)

⇒ ЕК - средняя линия (по определению)

Средняя линия равна половине основания.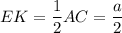

⇒ $\displaystyle EK = \frac{1}{2}AC=\frac{a}{2}$

3. Рассмотрим ΔАЕК.

АО = ОК; ОН || ЕК.

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок - средняя линия этого треугольника.

⇒ ОН - средняя линия ΔАЕК.

$\displaystyle OH=\frac{1}{2}EK=\frac{1}{2}*\frac{a}{2}=\frac{a}{4}$