Отрезки АД и ВС пересекаются в точке О, являющейся серединой каждого из них. Докажите, что треугольник АОВ равен треугольнику ДОС. Найдите сторону СД и угол ОВА, если угол ОСД равен 50°,а отрезок АВ равен 10 см

Показать ответ

Ответ:

GoriachiyKirill

17.04.2022 13:13

Найди площадь круга, вписанного в равнобедренную трапецию с основаниями длиной 6 см и 12 см и периметром 36 см

Объяснение:

АВСМ- описанная трапеция⇒ суммы длин противоположных сторон равны. Т.е 6+12=АВ+СМ⇒ АВ=СМ=9 см. Пусть ВК⊥АМ , СР⊥АМ.

S(круга)=πr². Радиус вписанной в трапецию окружности будет равен половине высоты трапеции.

Т.к. ВК⊥АМ , СР⊥АМ, то КВСР-прямоугольник ⇒

КР=6 см, АК=РМ=(12-6) :2=3 (см).

ΔАВК-прямоугольный, по т. Пифагора :

ВК=√(9²-3²)=√((9-3)(9+3))=√(6*12)=6√2(см).

ВК-высота трапеции, значит r=3√2 см.

S(круга)= π (3√2 )²=18π (см²).

Подробнее - на -

0,0(0 оценок)

Ответ:

qwweee

07.12.2022 08:09

Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.

$13x+4y-7=13\cdot 5+4\cdot (-3)-7=46\ne 0\\\\2x-y-1=2\cdot 5-(-3)-1=12\ne 0$

Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.

BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: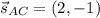 $\vec{s}_{AC}=(2,-1)$ .

Точка А(5,-3)∈АС и уравнение АС имеет вид:

$\frac{x-5}{2}=\frac{y+3}{-1}\; \; ,\; \; -x+5=2y+6\; \; ,\; \; \underline {x+2y+1=0}$

CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: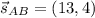 $\vec{s}_{AB}=(13,4)$ .

Точка А(5,-3)∈АВ и уравнение АВ имеет вид:

$\frac{x-5}{13}=\frac{y+3}{4}\; \; ,\; \; 4x-20=13y+39\; \; ,\; \; \underline {4x-13y-59=0}$

Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .

$B:\; \left \{ {{4x-13y=59\qquad } \atop {2x-y=1\, |\cdot (-2)}} \right.\oplus \left \{ {{-11y=57} \atop {2x=y+1}} \right. \; \; \left \{ {{y=-\frac{57}{11}} \atop {2x=-\frac{46}{11}}} \right.\; \; \left \{ {{y-\frac{57}{11}} \atop {x=-\frac{23}{11}}} \right. \; \; B(-\frac{23}{11}\, ,\, -\frac{57}{11})\\\\\\C:\; \left \{ {{x+2y=-1\, |\cdot (-2)} \atop {13x+4y=7\qquad }} \right.\oplus \left \{ {{2y=-x-1} \atop {11x=9\quad }} \right. \; \; \left \{ {{2y=-\frac{20}{11}} \atop {x=\frac{9}{11}}} \right.\; \left \{ {{y=-\frac{10}{11}} \atop {x=\frac{9}{11}}} \right.\; \; C(\frac{9}{11}\, ,\, -\frac{10}{11})$