ответить на вопросы 1)Точки А,В и С лежат на окружности. Сколько плоскостей проходит через эти точки?
А)ни одной
Б)одна
В)бесконечное множество
Г)две
2)АВСD - параллелограмм. О - точка пересечения диагоналей этого параллелограмма. Сколько плоскостей проходит через точки А, С и О?
А)две
Б)ни одной
В)бесконечное множество
Г)одна
3) Сколько общих точек имеют прямая и плоскость, если они пересекаются?
А)две
Б)ни одной
В)одну
Г)бесконечное множество
4) Сколько общих точек имеют прямая и плоскость, если прямая лежит в плоскости?
А)бесконечное множество
Б)ни одной
В)две
Г)одну
5) Сколько общих точек могут иметь две плоскости? (выберите все верные ответы)
А)ни одной
Б)одну
В)две
Г)бесконечное множество
6) Выберите возможные задания плоскости (укажите все варианты)
А)три точки, не лежащие на одной прямой
Б)прямая и не лежащая на ней точка
В)две пересекающиеся прямые
Г)две параллельные прямые
7) АВСD - параллелограмм. Прямая AD пересекает данную плоскость. Сколько общих точек имеют прямая ВС и данная плоскость?
А)одну
Б)ни одной
В)бесконечное множество
Г)две
8) АВСD - параллелограмм. Прямая AD параллельная данной плоскости. Сколько общих точек имеют прямая ВС и данная плоскость? (выберите все возможные варианты)
А)одну
Б)бесконечное множество
В)ни одной
Г)две

Показать ответ

Ответ:

kelaruu

13.12.2021 14:49

Любая линейная функция выражается формулой y = kx + b. Подставим известные нам значения x и y из точек в эту формулу и составим систему:

$\left \{ {-1k + b = 1} \atop {-4k + b = 4} \right.$

Вычтем из второго уравнения первое и найдём k:

(-4k + b) - (-1k + b) = - 4k + b + 1k - b = -3k

$-3k = 3\\k = -1$

Подставим найденный k в любое уравнение линейной функции из системы, чтобы найти b:

$- 4 * (-1) + b = 4\\4 + b = 4\\b = 0$

Таким образом, уравнение первой линейной функции f (x) выглядит как y = -1x + 0, или, упрощая, y = - x.

Повторим те же действия с точками функции g (x). Составляем систему:

$\left \{ {{2k + b = 7} \atop {-2k + b = -1}} \right.$

На этот раз проще будет сначала найти b, так как это можно сделать сложением двух уравнений:

2k + b + (-2k + b) = 2k + b - 2k + b = 2b

$2b = 6\\b = 3$

Подставляем в уравнение из системы:

$2k + 3 = 7\\2k = 4\\k = 2$

Таким образом, уравнение второй линейной функции g (x) выглядит как y = 2x + 3.

Чтобы найти точку пересечения графиков линейных функций, необходимо приравнять их формулы друг к другу, чтобы найти общую абсциссу. Получаем:

$- x = 2x + 3\\- 3x = 3\\x = - 1$

Найдём значение ординаты y в точке пересечения по любой из формул:

$y = -x\\y = - (-1)\\y = 1$

Таким образом, графики функций f (x) и g (x) пересекаются в точке (- 1; 1).

0,0(0 оценок)

Ответ:

nastyazhovnirenko

04.02.2020 04:37

Внутри правильного треугольника со стороной √3 выбрана произвольная точка . Чему равна сумма расстояний от этой точки до сторон треугольника ?

Объяснение:

Пусть точка Р-произвольная. Опустим на стороны правильного ΔАВС перпендикуляры . Обозначим их х,у,z ( кстати, получили педальный треугольник, если соединить основания перпендикуляров).

S(ABC)=S( PAB)+S(PBC)+S(PAC).

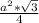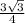S(ABC)=S(равн. тр)= $\frac{a^{2}*\sqrt{3} }{4}$ = $\frac{3\sqrt{3} }{4}$ ,