Точка S одинаково удалена от вершин квадрата, => можем рассматривать правильную четырехугольную пирамиду SABCD. AS=BS=CS=DS= 30 см, SO=24 см, SO_|_ABCD. О - точка пересечения диагоналей квадрата - основания пирамиды.
рассмотрим ΔAOS: <AOS=90°, гипотенуза AS=30 см катет SO=24 см катет AO, найти по теореме Пифагора: AS²=AO²+SO² 30²=AO²+24², AO²=30²-24². 30²-24²=(30-24)*(30+24)=6*54=6*6*9 AO=6*3, AO=18 см AO=AC/2. AC диагональ квадрата, АС=36 см AC²=2a², a - сторона квадрата 36²=2*а². а=18√2
Объяснение:
Дано: АВСD - равнобедренная трапеция, АС⊥ВD, КМ - высота трапеции, КМ=12 см, АВ=СD=15 см.
Найти: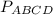
Рассмотрим ΔOBC и ΔAOD. Они прямоугольные, т.к. ∠BOC=∠AOD=90°.
В равнобедренной трапеции диагонали равны, а высота, проведенная через точку пересечения диагоналей является осью симметрии трапеции.
Следовательно ВО=ОС и АО=OD.
Значит ΔOBC и ΔAOD равнобедренные.
ОК - медиана ΔOBC, проведенная из вершины прямого угла. Следовательно ВК=КС=КО.
ОМ - медиана ΔAOD, проведенная из вершины прямого угла.
Следовательно ОМ=АМ=МD.
КМ=КО+ОМ=ВК+АМ.
ВК+АМ - это полусумма оснований.
Значит сумма оснований трапеции будет в два раза больше КМ, т.е. ее высоты.
ВС+АD = 2*МК = 2*12 = 24
AS=BS=CS=DS= 30 см, SO=24 см, SO_|_ABCD. О - точка пересечения диагоналей квадрата - основания пирамиды.
рассмотрим ΔAOS:
<AOS=90°,
гипотенуза AS=30 см
катет SO=24 см
катет AO, найти по теореме Пифагора:
AS²=AO²+SO²
30²=AO²+24², AO²=30²-24². 30²-24²=(30-24)*(30+24)=6*54=6*6*9
AO=6*3, AO=18 см
AO=AC/2. AC диагональ квадрата, АС=36 см
AC²=2a², a - сторона квадрата
36²=2*а². а=18√2
ответ: сторона квадрата AB=18√2 см