Аксиома - это утверждение о свойствах геом.фигур, принимаемое без доказательства. Например: через любые две точки можно провести прямую и при том только одну.
Обратная теорема - это утверждение, в котором условие исходной теоремы (прямого утверждения) поставлено заключением, а заключение — условием. Например: теорема - если два угла смежные, их сумма равна 180 градусов, а обратная ей - если сумма двух углов равна 180 градусов, то эти углы смежные.
Р(0; -44)
Объяснение:
1) Представим координаты точки K как (х₁; у₁), точки М как (х₂; у₂), точки P как (х₃; у₃)
Найдём разницу соответствующих координат точек М и К:
Δх = (х₂ - х₁) = 4-6 = -2
Δу = (у₂ - у₁) = -8 - 10 = -18
Эти величины показывают нам как изменяется координата точки на отрезке, в зависимости от удаления т.М от т. K.
Так как известно, что т. М делит отрезок РК в отношении 2:1, начиная от т. Р, то коэффициент соотношения длин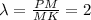 .
.
Тогда и изменение (дельта) координат от т.М до т.Р будет больше в 2 раза. Значит для вычисления координат т. Р можно записать выражения:
Аксиома - это утверждение о свойствах геом.фигур, принимаемое без доказательства. Например: через любые две точки можно провести прямую и при том только одну.
Теорема - это утверждение, требующее доказательства. Например: теорема Пифагора - квадрат гипотенузы равен сумме квадратов катетов.
Обратная теорема - это утверждение, в котором условие исходной теоремы (прямого утверждения) поставлено заключением, а заключение — условием. Например: теорема - если два угла смежные, их сумма равна 180 градусов, а обратная ей - если сумма двух углов равна 180 градусов, то эти углы смежные.