по условию известно, что в круговой конус вписана правильная четырехугольная пирамида, => d диагональ квадрата, основания пирамиды = D диаметру основания конусаD=2R, D^2=(2R)^2D^2=4R^2d^2=2×(2R^2)d^2=2×625, d^2=1250рассмотрим прямоугольный треугольник:d диагональ квадрата - гипотенузаа сторона квадрата - катета сторона квадрата - катетпо теореме Пифагора:
сторона квадрата а=25
Объяснение:
объем конуса:
V=(1/3)×S осн×Н
V=(1/3)×πR^2H
по условию известно, что
V=625π
H=6
уравнение:
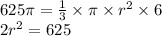
по условию известно, что в круговой конус вписана правильная четырехугольная пирамида, => d диагональ квадрата, основания пирамиды = D диаметру основания конусаD=2R, D^2=(2R)^2D^2=4R^2d^2=2×(2R^2)d^2=2×625, d^2=1250рассмотрим прямоугольный треугольник:d диагональ квадрата - гипотенузаа сторона квадрата - катета сторона квадрата - катетпо теореме Пифагора: