ответ.
Треугольная пирамида , все её грани равны , так как все грани -
прямоугольные треугольники с равными катетами : AD=AB=AC ,
∠СAD=∠BAD=∠САВ=90° .
Обозначим катеты через а . Тогда площадь одной грани равна . А площадь полной поверхности равна сумме площадей
трёх одинаковых граней , то есть .
Найдём квадрат катета:
Найти надо ВС - гипотенузу прямоугольного треугольника с катетами, равными а . По теореме Пифагора имеем
ответ.
Треугольная пирамида , все её грани равны , так как все грани -
прямоугольные треугольники с равными катетами : AD=AB=AC ,
∠СAD=∠BAD=∠САВ=90° .
Обозначим катеты через а . Тогда площадь одной грани равна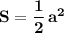 . А площадь полной поверхности равна сумме площадей
. А площадь полной поверхности равна сумме площадей
трёх одинаковых граней , то есть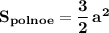 .
.
Найдём квадрат катета:
Найти надо ВС - гипотенузу прямоугольного треугольника с катетами, равными а . По теореме Пифагора имеем