Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.
АВ=ВС=21см
Рассмотрим прямоугольный ΔAВD(∠D=90°)
По теореме Пифагора найдём катет AD:
В равнобедренном треугольнике высота, проведенная к основанию, является так же и медианой: AD=DC
AC=2*AD=2*20.88=41.76 cм
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе:
По таблице синусов находим значение угла А:
∠ А ≅ 6°
В равнобедренном треугольнике углы при основании равны.
41.76 cм
6°
6°
168°
Объяснение:
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.АВ=ВС=21см
Рассмотрим прямоугольный ΔAВD(∠D=90°)
По теореме Пифагора найдём катет AD:
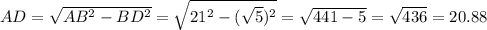
В равнобедренном треугольнике высота, проведенная к основанию, является так же и медианой: AD=DCAC=2*AD=2*20.88=41.76 cм
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе:По таблице синусов находим значение угла А:
∠ А ≅ 6°
В равнобедренном треугольнике углы при основании равны.∠С = ∠ А ≅ 6°
Сумма углов треугольника равна 180°
∠В = 180-∠А-∠С = 180-6-6=168°
1-б 2-а 3 в
Объяснение:
1) угол А1 смежный с углом А2, следовательно его мы можем найти так:180-110=70
Угол С мы можем найти исходя из того, что сумма углов треугольника 180:180-70-40=70
2)угол В1 смежный с углом В2, следовательно его мы можем найти так: 180-160=20
По рисунку видно что второй угол 90 градусов.
Угол А мы можем найти исходя из того, что сумма углов треугольника:180-50-90=40
3) угол С1 смежный с углом С2, следовательно его мы можем найти так:180-150=30
По рисунку видно, что треугольник равнобедренный=>, углы при основании равнв(С=А) =>В=180-(30*2)=120