1) Все стороны ромба ABCD равны, поэтому каждая равна 53/4.
2) Диагонали AC и BD ромба ABCD взаимно перпендикулярни и по свойству параллелограмма точкой O пересечения делятся пополам.Поэтому половины диагоналей ромба (образующие прямой угол) также относятся как 2:7, т.е. АО:ОВ = 2:7.
3) Пусть t - длина некоторого отрезка. Тогда по теореме Пифагора
Значит, АО=
BO=
4) Площадь ромба равна половине произведения диагоналей. А с др. стороны, она равна произведению стороны на высоту к этой стороне. Отсюда
1) Все стороны ромба ABCD равны, поэтому каждая равна 53/4.
2) Диагонали AC и BD ромба ABCD взаимно перпендикулярни и по свойству параллелограмма точкой O пересечения делятся пополам.Поэтому половины диагоналей ромба (образующие прямой угол) также относятся как 2:7, т.е. АО:ОВ = 2:7.
3) Пусть t - длина некоторого отрезка. Тогда по теореме Пифагора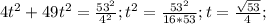
Значит, АО=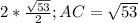
BO=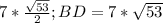
4) Площадь ромба равна половине произведения диагоналей. А с др. стороны, она равна произведению стороны на высоту к этой стороне. Отсюда
Латиница заменена на русские
Треугольник ДЕФ, Медиана ЕК = 1/2 х корень (2 х ДЕ в квадрате + 2 х ЕФ в квадрате -
- ДФ в квадрате) = 1/2 х корень (224+288-256)=1/2 х 16=8
Треугольники ДКЕ и ЕКФ равнобедренные КФ=КЕ=ДК=8
cos углаФ = (ЕФ в квадрате + КФ в квадрате - КЕ в квадрате) / 2 х КФ х ЕФ =
= (144 + 64 - 64) / 2 х 8 х 12 = 144/192=0,75, что отвечает углу 41 град = углу КЕФ,
угол КДЕ=углуДЕК = а
а + а + 41 + 41 = 180 град, а=49 =угол КДЕ=углуДЕК
угол Е = угол ДЕК+угол КЕФ=49+41=90, треугольник ДЕФ - прямоугольный, ДФ -гипотенуза
радиус вписанной окружности = (ДЕ х ЕФ) / (ДЕ + ЕФ + ДФ) = 4 х корень7 х 12 / (4 х корень7 + 12 +16) = 4 х 2,65 х 12 / (4 х 2,65 + 12 +16) = 127,2/38,6=3,3