Рисунок не могу. Площадь боковой поверхности цилиндра Sбок = 2πRH, где R - радиус, Н – высота цилиндра. Проведем из центра цилиндра до концов хорды радиусы, так как дуга 90°, то радиусы расположены под углом в 90°, ми имеем прямоугольный равнобедренный треугольник, в котором хорда – гипотенуза. Применим теорему Пифагора c^2 = a^2 + b^2, a = b = R, c^2 = 2·R^2, R = c/√2 , = 8√2 /√2 = 8 (см). Теперь найдем высоту. Хорда, диагональ сечения и высота образуют прямоугольный треугольник, в котором хорда и высота – катеты. Найдем катет через другой катет Н = 82·tg 60° = 8√2·√3 = 8√6 (см). Sбок = 2π·8·8√6 = 128√6π
Раз призма правильная треугольная, значит в основании лежит правильный треугольник.
Площадь правильного треугольника рассчитывается по формуле:
Сторона основания - это и есть сторона правильного треугольника. Значит, а = 6.
Площадь одного основания будет равна:
Таких оснований в призме два, значит сумма их площадей будет равна:
=
Боковая поверхность призмы складывается из площадей трех четырехугольников. Площадь каждого четырехугольника равна произведению высоты призмы на сторону основания: h*a = 6*h.
Площадь боковой поверхности призмы арвна:
3*6*h = 18*h.
площадь боковой поверхности призмы равна сумме площадей ее оснований. Приравниваем обе суммы, получаем уравнение:
= 18*h.
Решаем уравнение:
h = .
Высота, то есть длина бокового ребра призмы равна .
Рисунок не могу. Площадь боковой поверхности цилиндра Sбок = 2πRH, где R - радиус, Н – высота цилиндра. Проведем из центра цилиндра до концов хорды радиусы, так как дуга 90°, то радиусы расположены под углом в 90°, ми имеем прямоугольный равнобедренный треугольник, в котором хорда – гипотенуза. Применим теорему Пифагора c^2 = a^2 + b^2, a = b = R, c^2 = 2·R^2, R = c/√2 , = 8√2 /√2 = 8 (см). Теперь найдем высоту. Хорда, диагональ сечения и высота образуют прямоугольный треугольник, в котором хорда и высота – катеты. Найдем катет через другой катет Н = 82·tg 60° = 8√2·√3 = 8√6 (см). Sбок = 2π·8·8√6 = 128√6π
Раз призма правильная треугольная, значит в основании лежит правильный треугольник.
Площадь правильного треугольника рассчитывается по формуле:
Сторона основания - это и есть сторона правильного треугольника. Значит, а = 6.
Площадь одного основания будет равна:
Таких оснований в призме два, значит сумма их площадей будет равна:
Боковая поверхность призмы складывается из площадей трех четырехугольников. Площадь каждого четырехугольника равна произведению высоты призмы на сторону основания: h*a = 6*h.
Площадь боковой поверхности призмы арвна:
3*6*h = 18*h.
площадь боковой поверхности призмы равна сумме площадей ее оснований. Приравниваем обе суммы, получаем уравнение:
Решаем уравнение:
h =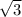 .
.
Высота, то есть длина бокового ребра призмы равна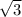 .
.