Построить правильный шетсиуголтник поворот на 120 градусов по часовой стрелке. Нужен рисунок!

Показать ответ

Ответ:

nikitka1011

20.12.2022 20:49

94. а).Дано: Док-во:
АВ=АС. 1).L1=L2(по условию)
L1=L2. 2).AB=AC(по условию)
Доказать: 3).AD-общая сторона
АВD=АСD. =>ABD=ACD по 2 сторонам и углу между ними
б).Дано: Решение:
АС=15 см. Т.к BD=DC,AB=AC,то
DC=5 см. ВD=5 см
Найти: АВ=15 см
ВD,AB-? ответ:5 см,15 см.
95. а).Дано:   Док-во:
ВC=АD. 1). АС-общая сторона АВС и СDA
L1=L2. 2).BC=AD,L1=L2( по условию)
Доказать:    =>ABC=CDA по 2 сторонам и углу между ними
АВС=СDА
б).Дано: Решение:
AD=17 см. Т.к. АB=DC,BC=AD,то
DC=14 см. АВ=14 см
Найти: ВС=17 см
АВ,ВС-? ответ:14 см,17 см.

0,0(0 оценок)

Ответ:

valikromanenkop074w0

03.03.2022 11:45

Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.

$13x+4y-7=13\cdot 5+4\cdot (-3)-7=46\ne 0\\\\2x-y-1=2\cdot 5-(-3)-1=12\ne 0$

Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.

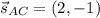BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: $\vec{s}_{AC}=(2,-1)$ .

Точка А(5,-3)∈АС и уравнение АС имеет вид:

$\frac{x-5}{2}=\frac{y+3}{-1}\; \; ,\; \; -x+5=2y+6\; \; ,\; \; \underline {x+2y+1=0}$

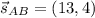CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: $\vec{s}_{AB}=(13,4)$ .

Точка А(5,-3)∈АВ и уравнение АВ имеет вид:

$\frac{x-5}{13}=\frac{y+3}{4}\; \; ,\; \; 4x-20=13y+39\; \; ,\; \; \underline {4x-13y-59=0}$

Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .

$B:\; \left \{ {{4x-13y=59\qquad } \atop {2x-y=1\, |\cdot (-2)}} \right.\oplus \left \{ {{-11y=57} \atop {2x=y+1}} \right. \; \; \left \{ {{y=-\frac{57}{11}} \atop {2x=-\frac{46}{11}}} \right.\; \; \left \{ {{y-\frac{57}{11}} \atop {x=-\frac{23}{11}}} \right. \; \; B(-\frac{23}{11}\, ,\, -\frac{57}{11})\\\\\\C:\; \left \{ {{x+2y=-1\, |\cdot (-2)} \atop {13x+4y=7\qquad }} \right.\oplus \left \{ {{2y=-x-1} \atop {11x=9\quad }} \right. \; \; \left \{ {{2y=-\frac{20}{11}} \atop {x=\frac{9}{11}}} \right.\; \left \{ {{y=-\frac{10}{11}} \atop {x=\frac{9}{11}}} \right.\; \; C(\frac{9}{11}\, ,\, -\frac{10}{11})$