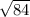Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
нам сейчас известна только одна диагональ АС =4(ОС*2), а чтобы найти площадь нужно знать две(диагонали). через теорему пифагора мы найдем вторую диаглналь. с^2=a^2+b^2, b^2=c^2-a^2, b^2=c^2(гипотенуза, в нашем случае это ВС равное 5)-a^2(это ОС равное 2) то есть в^2= 25(это 5 в квадрате) - 4(2 в квадрете) = 21(так и записывай в= корень из 21), вторая диагональ= 2*= корень(4*21)=корень(84). теперь чтобы найти площадь нужно (д1*д2)/2. получается (4*корень(84))/2. запишешь в форме дроби, ото 4 и 2 можно сократить, останется 2
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
тут площадь ромба находится через диагонали.
Объяснение:
нам сейчас известна только одна диагональ АС =4(ОС*2), а чтобы найти площадь нужно знать две(диагонали). через теорему пифагора мы найдем вторую диаглналь. с^2=a^2+b^2, b^2=c^2-a^2, b^2=c^2(гипотенуза, в нашем случае это ВС равное 5)-a^2(это ОС равное 2) то есть в^2= 25(это 5 в квадрате) - 4(2 в квадрете) = 21(так и записывай в= корень из 21), вторая диагональ= 2*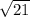
= корень(4*21)=корень(84). теперь чтобы найти площадь нужно (д1*д2)/2. получается (4*корень(84))/2. запишешь в форме дроби, ото 4 и 2 можно сократить, останется 2