Прямоугольные треугольники, изображенные на рисунке, будут равны
90
Укажите правильный вариант ответа
o
По катету и прилежащему к нему острому углу;
o
по гипотенузе и острому углу;
o
по ДЕЗуМ Катетам,
o
по катету и гипотенузе,​

Дано:

ΔАВС - равнобедренный (АВ и ВС - боковые стороны).

Р(ΔАВС) = 25 см.

Разность двух сторон = 4 см.

Найти:

АВ = ?

ВС = ?

АС = ?

1) Итак, разность боковых сторон АВ и ВС не может быть равна 4 см, так как они равны, и при вычитании должны давать 0.

Тогда, только остаётся, что разность основания АС и боковой стороны АВ = 4 см.

Пусть боковые стороны АВ и ВС = х, а основание АС = у.

Составим систему -

АВ = ВС = х = 7 см.

АС = у = 11 см.

2) Но стоп, вдруг боковая сторона больше основания, тогда получится, что разность боковой стороны АВ и основания АС = 4 см!

Составим новую систему -

АВ = ВС = х = 29/3 см.

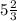АС = у = см.

ответ: 7 см, 7 см, 11 см или 29/3 см, 29/3 см, 5+(2/3) см.

1. Написать уравнение окружности в общем виде, изобразить на координатной плоскости.

2. Выполнив построение, выясните взаимное расположение окружности и прямой, заданных уравнениями:

у=(х+2)2+(у+1) 2=4   ,у= –х+1  .В ответе написать пересекаются, не пересекаются, касаются

3. Написать окружности прямой, с центром в точке О(1;1) и радиусом 2 см.

Объяснение:

1.Уравнение окружности (x – х₀)²+ (y – у₀)² = R²   , где (х₀; у₀)-координаты центра.

2. (х+2)²+(у+1) ²=4  окружность с центром в точке (-2;-1) , радиусом 2

у= –х+1  

(х+2)²+(-х+1+1) ²=4  

(х+2)²+(2-х) ²=4  

х²+4х+4+4-4х+х²=4  

2х²=-8 или х²=-4 корней нет ⇒ не пересекаются.

3)  (x – 1)²+ (y – 1)² =4