Для нахождения производной, воспользуемся двумя формулами:
1) при нахождении производной разности, нужно помнить, что производная разности равна разности производных. (u - v)' = u' - v'. Если немного запутано, то когда будешь смотреть пример, то, думаю, поймёшь. 2) ( 3) (cosx)' = - sinx
Сначала перепишем за знак производной константу 2 (2 - число, которое не может просто взять и измениться само по себе - константа) и поставим знак умножения, дальше нас интересует нахождение производной от . По формуле, которую я записала выше, мы можем увидеть, что показатель степени 6 мы записываем перед х (становится множителем), но х не остаётся без показателя степени, по формуле записано n - 1, то есть в нашем случае это 6 - 1 ( = 5), то есть х становится в 5й степени.
С косинусом даже легче: производная косинуса (по формуле) равна синусу, но обязательно со знаком минус, т.е. - sinx
Третий момент, на который нужно обратить внимание, - то, что перед косинусом первоначально был минус. При нахождении производной получается - (-sinx), если перед скобкой стоит минус, то знак в скобках меняется, поэтому в ответе становится + sinx.
Так как в условии не оговорено положение точки М, будем считать ее серединой любой из сторон треугольника АВС. Приведенное решение только для условия с этим предположением.
Сделаем дополнительные построения: соединим вершину перпендикуляра D с вершинами треугольника АВС. Тогда получится правильная пирамида АВСD с боковыми ребрами DA=DB=DC (так как точка О - центр правильного треугольника АВС, то отрезки DA, DB и DC равны, как наклонные к плоскости, проведенные из одной точки, проекции которых равны - радиусы описанной окружности ).
Соединим точку М с противоположной вершиной С. Тогда МС - высота правильного треугольника АВС и по его свойствам МС - высота и медиана.
Следовательно, точка О делит отрезок МС в отношении 2:1, считая от вершины С. Треугольник DOM - пифагоров и МО=3. Тогда ОС=6, а DC=√(DO²+OC²) = √(16+36) = √52 = 2√13.
Найдем сторону треугольника АВС. МС=МО+ОС = 3+6=9. Из прямоугольного треугольника АМС по Пифагору: МС² = АС²- АС²/4 => 81*4=3*АС² => АС=6√3. Тогда периметр треугольника АВС равен 18√3 ед.
y' = 12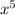
+ sinx
Объяснение:
Для нахождения производной, воспользуемся двумя формулами:
1) при нахождении производной разности, нужно помнить, что производная разности равна разности производных. (u - v)' = u' - v'. Если немного запутано, то когда будешь смотреть пример, то, думаю, поймёшь. 2) (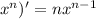
3) (cosx)' = - sinx
у = 2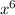
- cosx
y' = (2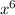
- cosx)' = (2 · 
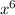)' - (cosx)' = 2 · (
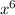)' - (cosx)' = 2 · 6
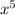- (-sinx) = 12
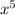+ sinx
Попробую ещё немного объяснить:
Как получить производную от 2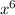
Сначала перепишем за знак производной константу 2 (2 - число, которое не может просто взять и измениться само по себе - константа) и поставим знак умножения, дальше нас интересует нахождение производной от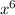
. По формуле, которую я записала выше, мы можем увидеть, что показатель степени 6 мы записываем перед х (становится множителем), но х не остаётся без показателя степени, по формуле записано n - 1, то есть в нашем случае это 6 - 1 ( = 5), то есть х становится в 5й степени.
С косинусом даже легче: производная косинуса (по формуле) равна синусу, но обязательно со знаком минус, т.е. - sinx
Третий момент, на который нужно обратить внимание, - то, что перед косинусом первоначально был минус. При нахождении производной получается - (-sinx), если перед скобкой стоит минус, то знак в скобках меняется, поэтому в ответе становится + sinx.
Если ещё есть вопросы, задавай в комментариях.
Так как в условии не оговорено положение точки М, будем считать ее серединой любой из сторон треугольника АВС. Приведенное решение только для условия с этим предположением.
Сделаем дополнительные построения: соединим вершину перпендикуляра D с вершинами треугольника АВС. Тогда получится правильная пирамида АВСD с боковыми ребрами DA=DB=DC (так как точка О - центр правильного треугольника АВС, то отрезки DA, DB и DC равны, как наклонные к плоскости, проведенные из одной точки, проекции которых равны - радиусы описанной окружности ).
Соединим точку М с противоположной вершиной С. Тогда МС - высота правильного треугольника АВС и по его свойствам МС - высота и медиана.
Следовательно, точка О делит отрезок МС в отношении 2:1, считая от вершины С. Треугольник DOM - пифагоров и МО=3. Тогда ОС=6, а DC=√(DO²+OC²) = √(16+36) = √52 = 2√13.
Найдем сторону треугольника АВС. МС=МО+ОС = 3+6=9. Из прямоугольного треугольника АМС по Пифагору: МС² = АС²- АС²/4 => 81*4=3*АС² => АС=6√3. Тогда периметр треугольника АВС равен 18√3 ед.
ответ: Рabc = 18√3. AD=BD=DC = 2√13 ед.