Решите 11 и 12
11) найти : p-ftse
12) найти p - lmnk

AM ⊥BM ( AB диаметр большой окружности )
OC ⊥ BM ( OC ⊥ BC ,где  O центр малой окружности , BC касательная) ⇒ AM | | OC .  MC/CB= AO/OB  (обобщенная теорема Фалеса) .  
2,4 /4 =r/(2R -r) ⇔   r=3R/4   (1) .
Из ΔBCO  по теореме Пифагора :
OB² - OC² =BC² ;
(2R -r)² - r² = 4² ⇔ 4R(R-r) =16  ⇔ R(R-r) =4   (2).
R(R -3R/4) =4 ⇒  R =4. ⇒  r=3R/4 = 3.

AD =AC+CD.
AM =√(AB² -BM²) =√((2R)² -(MC+CB)² ) =√(8² -6,4²) =√(8 -6,4)(8 +6,4) =4,8.  
AM можно вычислить по другому: AM/OC =MB/CB ⇔ AM/3 =6,4/4⇒
AM =4,8.
---
AC =√(BC² +AM²) =√(2,4² +4,8²) =√(2,4² +(2*2,4)²)  = 2,4√5. 
AC*CD = MC*BC ⇔ 2,4√5 *CD =2,4*4⇒ CD =4/√5 =4√5 / 5 =0,8√5.
AD =AC+CD= 2,4√5 + 0,8√5  =3,2√5 .

Задача 6

В ΔАВС , АВ=ВС, АЕ -биссектриса, Е∈ВС. Найти Р( АВС), если ВС-АС=8 и ВЕ:ЕС=3:2.

Решение.

Пусть одна часть х. Тогда ВЕ=3х, ЕС=2х ⇒ ВС=5х ⇒ АВ=5х , т.к треугольник равнобедренный.

По т. о биссектрисе треугольника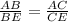    , тогда 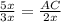⇒ AC= .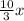

По условию  ВС-АС=8 , поэтому 5х-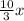 = 8  или  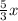 =8  или х=4,8.

ВС=5*4,8=24 , АВ=24 , АС=.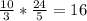

Р=24+24+16=64.

Задача 8

Стороны треугольника относятся как 2:3:3 . Найти периметр треугольника , если основание на 5 единиц меньше боковой стороны.

Решение .

Дан ΔАВС. АВ=ВС . Пусть одна часть х. Тогда АВ=ВС=3х, АС=2х .

По условию АС меньше АВ на 5, т.е  АВ-АС=5.

Получим 3х-2х=5 или х=5  . Тогда АВ=ВС=3*5=15, АС=2*5=10 .

Р=15+15+10=40.

Задача 9

Угол при вершине равнобедренного треугольника равен 120°. , высота , опущенная на основание,  равна 6 .Найти периметр треугольника .

Решение .

Дан ΔАВС , АВ=ВС  ,ВН⊥АС , ∠АВС=120°.

1) Высота равнобедренного треугольника является биссектрисой ⇒∠АВН=60° .

2) ΔАВН -прямоугольный , по свойству углов ∠А=90°-60°=30°.

Против угла в 30° , лежит катет равный половине гипотенузы , т.е ВН=1/2*АВ ⇒ АВ=12 ⇒ВС=12, т.к треугольник равнобедренный.

По т. Пифагора АН²=АВ²-ВН² или АН²=12²-6²  или АН=√18*6=6√3.

3) Высота равнобедренного ΔАВС является медианой, значит  АН=НС=6√3  ⇒АС =12√3.

4)Р=12√3+12+12=24+12√3.