Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Объяснение:
Пусть ∠АLК=α
1) ΔАКL -прямоугольный, tg∠АLК= , AL=в / tgα.
2)ΔACD -прямоугольный, АС=а√2, по т. Пифагора.
ΔКCD -прямоугольный, по т. Пифагора, КС=√(а²+(а-в)²).
Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Объяснение:
Пусть ∠АLК=α
1) ΔАКL -прямоугольный, tg∠АLК= , AL=в / tgα.
, AL=в / tgα.
2)ΔACD -прямоугольный, АС=а√2, по т. Пифагора.
ΔКCD -прямоугольный, по т. Пифагора, КС=√(а²+(а-в)²).
3)ΔACК, угол ∠АСК=α.
По т. косинусов выразим cosα :
АК²=АС²+КС²-2АС*КС*cosα,
в²=2а²+а²+(а-в)²-2*а√2*√(а²+(а-в)²)*cosα,
2*а√2*√(а²+(а-в)²)*cosα =-в²+2а²+а²+(а-в)² ,
2*а√2*√(а²+(а-в)²)*cosα =-в²+4а²-2ав+в² ,
2*а√2*√(а²+(а-в)²)*cosα =2а(2а-в) ,
cosα =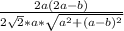
cosα = , tg²α=1:( cos²α)-1 , tgα =
, tg²α=1:( cos²α)-1 , tgα =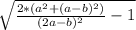 ,
,
tgα =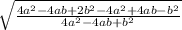 =
=
4)AL=в/tgα , AL=в: , AL=
, AL=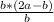 , AL=2a-b .
, AL=2a-b .
ответ: (3-sqrt(3))/(6*(1+sqrt(3))
Объяснение:
1. Найдем площадь треугольника АВС.
Проведем высоту ВН. Тогда АН=АС:2=2:2=1
Угол А=углу С=pi/6=180/6=30 градусов ( так как АВС- равнобедренный и АС- основание)
Тогда АВ=ВС= АН/cosA=1/cos30= 2/sqrt(3)
Тогда площадь треугольника АВС= S(ABC)= AB*AC*sinA/2=
=2*2/sqrt(3)/2/2=1/sqrt(3)= sqrt(3)/3
По свойству биссектрисы угла треугольника:
BЕ:ЕC=AB:AC => BD:DC= 2/sqrt(3): 2= 1: sqrt(3)
Тогда BЕ:BC= 1: (1+sqrt(3))
Тогда площадь треугольника АВЕ равна:
S(ABE)= S(ABC)* 1/(1+sqrt(3))= sqrt(3)/3/(1+sqrt(3)) (1)
Заметим , что поскольку AD - медиана, то площадь треугольника S(ADB)=1/2 *S(ABC)= sqrt(3)/6 (2)
Тогда площадь треугольника ADE нужно вычислять как разность площадей треугольников ABD и ABE. ( (2)- (1) )
S (ADE)= sqrt(3)/6- sqrt(3)/(3*(1+sqrt(3))=
=(sqrt(3)*(1+sqrt(3)- 2*sqrt(3))/(6*(1+sqrt(3))=
=(3+sqrt(3)-2*sqrt(3))/(6*(1+sqrt(3))=
=(3-sqrt(3))/(6*(1+sqrt(3))