Рисунок + решение радиус окружности,вписанной в основание правильной четырехугольной, пирамиды равен 8 корней из 2,высота пирамиды равна 8 корней из 2. найти: 1)апофему пирамиды 2)угол между боковой гранью и
основанием 3)площадь поверхности пирамиды 4)расстояние от центра основания пирамиды до плоскости боковой грани.
только рисунок не банить...модераторы...(
апофема-высота боковой грани правильной пирамиды SF=f=√(h²+r²)(по т пифагора)
сюда только радиус подставить и высоту
√(8√2+8√2)=√(128+128)=√256=16
2)угол между боковой гранью и основанием
в лс разберем..
3) площадь поверхности пирамиды
Sпов=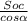
4)расстояние от центра основания пирамиды до плоскости боковой грани
___________
пусть ABCD основание, S -- вершина пирамиды, O -- центр основания, E -- середина AB
SO=8√2, SE=8√2
1)√(8√2+8√2)=√(128+128)=√256=16
2) SE и EO перпендикулярны AB, поэтому SEO -- искомый угол
tg SEO = SE/OE= 1, следовательно, SEO=45°
3) Площадь поверхности равна S=Sосн+Sбок
Sосн=AD^2
Sбок=4*(AB*SE)/2=2*AD*SE
4)разберем
5)в лс