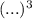с геометрией Три некомпланарных вектора a→, b→ и c→ размещены на рёбрах куба с общей вершиной. Точка E делит ребро AB так, что AE:EB=7:3, а точка F делит ребро CC1 так, что CF:FC1=1:1.

с геометрией Три некомпланарных вектора a→, b→ и c→ размещены на рёбрах куба с общей вершиной. Точка

Показать ответ

Ответ:

Максек1337

10.08.2020 03:24

Построение на рисунке в приложении.

Объяснение:

B1D -диагональ призмы. Точка Р - точка, лежащая на боковом ребре АА1 призмы, скрещивающимся с диагональю В1D.

Точки Р и В1 лежат в одной боковой грани. Соединяем их прямой РВ1. Точки Р и D лежат в одной боковой грани. Соединяем их прямой РD. Две параллельные грани пересекаются плоскостью сечения по параллельным прямым. Из точки D проводим луч, параллельный прямой РВ1 до пересечения с боковым ребром СС1 => получаем точку К на этом ребре (также скрещивающимся с диагональю B1D).

Соединив точки К и В1 получаем линию пересечения плоскости сечения с гранью ВВ1С1С (эта прямая будет параллельна прямой PD на грани AA1D1D). Четырехугольник (параллелограмм) PB1KD и будет искомым сечением.

Прикрепил фото задания,Нужно сделать 3 номер. Построить сечение четырехугольной призмы плоскостью ,п

0,0(0 оценок)

Ответ:

asetburkutov00

04.06.2020 01:40

Дано:

SABCD - Правильная четырёхугольная пирамида.

AB=8 (сторона основания)

$SA=2\sqrt{233}$ (боковое ребро)

SO=H - Высота

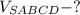
Найти: $V_{SABCD}-?$

1)В основании правильной четырёхугольной пирамиды лежит квадрат, а у квадрата все стороны равны, что говорить о том, что AB=BC=CD=AC=8

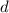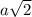2)Зная что диагональ равна $a\sqrt{2}$ , найдём .

$AC=d=a\sqrt{2}=8\sqrt{2}$

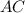Поскольку диагонали квадрата в точке их пересечения делятся пополам, найдём .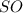

$SO=\frac{1}{2}*8\sqrt{2} =4\sqrt{2}$

3)Рассмотрим треугольник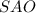 SAO , по рисунку видно, что он прямоугольный, поскольку 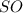высота из вершины S к плоскости основания. Тогда по теореме Пифагора наёдем высоту.