,с подробным решением: Сторона основания правильной четырехугольной призмы равна 8 см. Боковое ребро равно 10 см. Найдите площадь боковой поверхности, полную поверхность призмы и ее объем.
Сумма углов выпуклого n-угольника.-180(n-2) 2. четырехугольник является параллелограммом, если у него: 3 )две пары равных сторон3. трапеция называется равнобедренной, если у неё: 4)боковые стороны равны4. прямоугольником называется: 2)параллелограмм, у которого все углы прямые5. четырехугольник называется ромбом, если у него: 3)диагонали перпендикулярны и точкой пересечения делятся пополам 6. квадратом называется: 2)ромб, у которого все углы прямыевсякий прямоугольник является 4)параллелограммом 8. выберите верное утверждение: 1)истинно 2)ложно 3)истинно 4)ложно 9. внешний угол правильного n-угольника равен: 4)360/n10)многоугольник называется выпуклым, если 3)он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины..
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство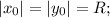
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)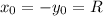 
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и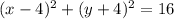
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили