С решением С точек A, Bi C, размещенных по одну сторону от
плоскости а, проведенные прямые, перпендикулярные
к плоскости а. Эти прямые пересекают прямую а
плоскости ав точках D, E IF соответственно. Найдите
длину отрезка BE, если AD = 6 см, СЭ = 9 см,
DE=EF.

Даны координаты вершин треугольника ABC

А(-4;10), В(8;1) , С(12;23) . Найти:  1) уравнение высоты CD и ее длину ;

2) уравнение медианы AE и координаты точки К , точки пересечения этой медианы с высотой CD.

Объяснение:

1) Прямые содержащие отрезки АВ и СD будут перпендикулярны , те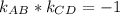

Уравнение прямой АВ 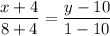   :    или 12(у-10)=-9(х+4) ,

4(у-10)=-3(х+4) , у-10= -0,75(х+4) ,  у= -0,75х+7.

Для уравнение прямой СD ,  у=4/3*х+b ,  найдем в используя координаты  С(12;23).

 ⇒ b=7.  Тогда уравнение высоты CD будет у=4/3*х+7.

CD=√( (12-х₂)²+(23-у₂)² ), где  C(12;23), D(х₂;у₂ )

Ищем координаты D

⇒      ⇒ x=0,y=7 . D(0;7)

СD=√( (12-0)²+(23-7)² )=√(144+256)=20.

2)Если АЕ-медиана , то Е середина ВС .

Е( (8+12):2 ; (1+23):2 ) или Е(10;12)

Уравнение прямой АЕ 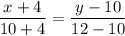   :    или 14(у-10)=2(х+4) ,

у-10=1/7*(х+4) , у-10= 1/7*х+4/7 ,  у=1/7*х+74/7.

Ищем координаты точки К

,    |*21  , 3x+74*3=28x+21*7 ,

25x=75 , x=3 . Тогда у= 1/7*(3+74)==11 ⇒ К(3;11).

Объяснение:

6

<3=х градусов

<2=(х-40) градусов

<2 и <3 смежные

Сумма смежных углов равна 180 градусов

<2+<3=180

Х-40+х=180

2х=180+40

2х=220

Х=110 градусов <3

<2=110-40=70 градусов

<1 =<2 =70 градусов - как внешние накрест лежащие

ответ : Б) 70 градусов

7

<2-<1=26

<2=26+<1

<2+<1=180 - как внутренние односторонние

26+<1+<1=180

2<1=180-26

2<1=154

<1=154:2

<1=77 градусов

<2=26+77=103 градусов

<3=<2 =103 градуса - как соответственные

<2+<3=103+103=206 градусов

ответ : В) 206 градусов