Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что . Проведем прямую . Тогда . Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. , а значит и любой прямой в этой плоскости. Пусть . Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда , а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость . Покажем, что . и , и . Тогда задача сводится к нахождению площади треугольника . Будем искать ее, как . Из подобия треугольников следует, что . Из подобия треугольников . Подставив найденное в формулу выше, получим . Таким нами образом было получено, что искомая площадь равна .
Обозначим вершины четырёхугольника АСВД, точка О – центр окружности, а пропорции 3х, 4х, 5х, 6х. Так как вся окружность составляет 360°, составим уравнение:
3х+4х+5х+6х=360
18х=360
х=360÷18
х=20°
Теперь найдём длину каждой дуги:
АВ=3х=3×20=60°
ВС=4х=4×20=80°
СД=5х=5×20=100°
АД=6х=6×20=120°
Теперь найдём каждый угол АВСД. Все углы четырёхугольника вписаны в окружность и каждый угол равен половине дуги на которую опирается:
∠А опирается на на дугуВД, которая включает в себя 2 дуги: ВС и СД.
ВД=ВС+СД=80+100=180°, тогда ∠А=180÷2=90°
∠В опирается на дугуАС:
АС=АД+СД=120+100=220° => ∠В=220÷2=110°
∠С опирается на дугуВД: ВД=АВ+АД=60+120=180° => ∠С=180÷2=90°
(см. объяснение)
Объяснение:
Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что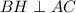
. Проведем прямую 
. Тогда 
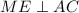. Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. 
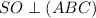, а значит и любой прямой в этой плоскости. Пусть 
. Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда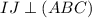 
, а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость 
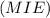. Покажем, что 
. 
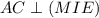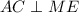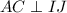и 
, и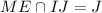 
. Тогда задача сводится к нахождению площади треугольника 
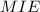. Будем искать ее, как 
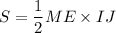. Из подобия треугольников следует, что 
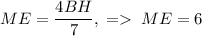. Из подобия треугольников 
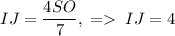. Подставив найденное в формулу выше, получим 
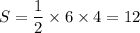. Таким нами образом было получено, что искомая площадь равна 
.
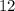Задание выполнено!
∠А=90°, ∠В=110°, ∠С=90°, ∠Д=70°
Объяснение:
Обозначим вершины четырёхугольника АСВД, точка О – центр окружности, а пропорции 3х, 4х, 5х, 6х. Так как вся окружность составляет 360°, составим уравнение:
3х+4х+5х+6х=360
18х=360
х=360÷18
х=20°
Теперь найдём длину каждой дуги:
АВ=3х=3×20=60°
ВС=4х=4×20=80°
СД=5х=5×20=100°
АД=6х=6×20=120°
Теперь найдём каждый угол АВСД. Все углы четырёхугольника вписаны в окружность и каждый угол равен половине дуги на которую опирается:
∠А опирается на на дугуВД, которая включает в себя 2 дуги: ВС и СД.
ВД=ВС+СД=80+100=180°, тогда ∠А=180÷2=90°
∠В опирается на дугуАС:
АС=АД+СД=120+100=220° => ∠В=220÷2=110°
∠С опирается на дугуВД: ВД=АВ+АД=60+120=180° => ∠С=180÷2=90°
∠Д опирается на дугуАС:
АС=АВ+ВС=60+80=140° => ∠Д=140÷2=70°
ПРОВЕРКА:
Сумма всех углов 4-угольника равна 360°:
∠А+∠В+∠С+∠Д=360°
90+110+90+70=200+160=360°