Высота Боковой грани с основанием 8 найдем из прямоугольного Δ где один катет - высота пирамиды, второй половина другой стороны 6:2=3, а гипотенуза искомая высота h₁ =√(6√2)²+3² =√72+9 =√81=9
Аналогично для другой боковой грани h₂=√(6√2)²+4² =√88=2√22
Площадь боковой поверхности равна площади двух треугольников с высотой h₁ и основанием 8 плюс двух треугольников с высотой h₂ и основанием 6 ⇒ S₁=9*8 + 2√22 * 6=72+12√22=12(6+√22)
Для определения площади всей поверхности добавим площадь основания- площадь прямоугольника 6х8=48 S= S₁+ 48= 12(6+√22)+48=12(10+√22)
Объем равен одной трети площади основания на высоту пирамиды V=1/3 *6√2 * 48=96√2
Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
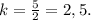
Площади подобных треугольников относятся как квадрат коэффициента подобия.Отсюда -
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
50 (ед²).
Высота Боковой грани с основанием 8 найдем из прямоугольного Δ где один катет - высота пирамиды, второй половина другой стороны 6:2=3, а гипотенуза искомая высота h₁ =√(6√2)²+3² =√72+9 =√81=9
Аналогично для другой боковой грани h₂=√(6√2)²+4² =√88=2√22
Площадь боковой поверхности равна площади двух треугольников с высотой h₁ и основанием 8 плюс двух треугольников с высотой h₂ и основанием 6 ⇒ S₁=9*8 + 2√22 * 6=72+12√22=12(6+√22)
Для определения площади всей поверхности добавим площадь основания- площадь прямоугольника 6х8=48 S= S₁+ 48= 12(6+√22)+48=12(10+√22)
Объем равен одной трети площади основания на высоту пирамиды V=1/3 *6√2 * 48=96√2