Схема дана с использованием схемы. *
а) Как вольтметр подключен к цепи?
б) Определить напряжение в цепи, ток в амперметре 1,2 А.
в) Сколько энергии выделяется, если цепь включить на 10 минут?
а) Как вольтметр подключен к цепи?
б) Определить напряжение в цепи, ток в амперметре 1,2 А.
в) Сколько энергии выделяется, если цепь включить на 10 минут?
Физика
Площадь равнобедренной трапеции равна полусумме оснований, умноженной на высоту.
Высота у нас уже есть Одно из оснований - тоже. Теперь надо найти большее основание. Если опустить высоту с меньшего основания на большее, то получим прямоугольный треугольник, где гипотенузой будет боковая сторона, одним из катетов - высота трапеции, а вторым катетом - часть основания трапеции. Чтобы узнать большее основание трапеции, нам нужно вычислить этот неизвестный катет в треугольнике, потому что длиной большего основания будет сумма двух таких катетов с меньшим основанием. Так как точно такой же треугольник можно получить, опустив высоту из другой точки меньшего основания трапеции. По теореме Пифагора вычисляем неизвестный катет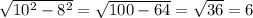
. Значит длина наибольшего катета равна 7+6+6=19 см.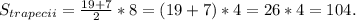 
При сворачивании точки А и В окажутся на противоположных сторонах окружности, так, что АВ будет диаметром окружности (которая поучается сечением цилиндра плоскостью, проходящей через А и В перпендикулярно оси). Почему? да просто PL станет окружностью (основанием цилиндра), а дуга АВ - это половина окружности.
Поскольку "несвернутый" треугольник АВС - равносторонний, то (внимание!) проекция "свернутого" треугольника на основание цилиндра будет равнобедренным треугольником (это следует из симметрии равностороннего треугольника), да еще - к тому же, как я уже сказал - опирающимся на диаметр. То есть это будет прямоугольный равнобедренный треугольник.
Кроме того, при сворачивании расстояние от точки С до плоскости сечения цилиндра через точки А и В не изменяется - сворачивание происходит вокруг оси, параллельной высоте "несвернутого" треугольника.
На самом деле, нам уже известно все, что надо, для вычисления площади "свернутого" треугольника АВС.
Пусть сторона квадрата равна 1. Тогда "несвернутая" АВ = 1/2, высота "несвернутого" АВС равна (1/2)*корень(3)/2 = корень(3)/4.
Сворачиваем. Сторона квадрата превращается в окружность, и "свернутая" АВ - её диаметр. То есть у полученной (в основании) окружности радиус 1/(2*пи), а диаметр АВ = 1/пи. "Свернутый" треугольник АВС при этом - равнобедренный, его высота к АВ равна расстоянию от точки С на поверхности цилиндра до середины диаметра АВ. При этом расстояние от С до плоскости АВ (перпендикулярной оси) равно высоте исходного "несвернутого" треугольника, то есть корень(3)/4, а расстояние от С до О определяется по теореме Пифагора
СО = корень((1/(2*пи))^2 + ((корень(3)/4)^2);
Площадь "свернутого" АВС равна
АВ*СО/2 = (1/2*пи)*корень((1/(2*пи))^2 + ((корень(3)/4)^2);
ну, поупрощайте... сильно не получится...