СЛУЧАЙНО ОТМЕТИЛА КАК ГЕОМЕТРИЯ ЗАРАНИЕ класс география все задания

5. Световые вспышки, проносящиеся по

темному небу - это:

а) астероиды

б) метеориты

в) кометы

г) метеоры

11. Глина и песок относятся к группе

горных пород:

а) органические

б) обломочные

в) метаморфические

г) магматические

12. Самый маленький материк: а) Южная Америка

б) Африка

в) Австралия

г) Северная Америка

13. Как называется непрерывный процесс

перемещения воды из Мирового

океана на сушу и обратно:

а) Мировой океан

б) приливы и отливы

в) воды суши

г) мировой круговорот воды

14. Внешняя сила Земли, образующая

рельеф:

а) извержение вулкана

б) ветер

в) землетрясение

г) движение магмы

15. Как называется материковая отмель: а) склон

б) рельеф

в) шельф

г) хребет

16. Самый большой по площади океан: а) Атлантический

б) Индийский

в) Северный Ледовитый

г) Тихий

17. 22 июня - это: а) день летнего солнцестояния

б) день осеннего равноденствия

в) день зимнего солнцестояния

г) день весеннего равноденствия

18. Условная линия, которая делит

Землю на северное и южное

полушария:

а) параллель

б) меридиан

в) экватор

г) градусная сеть

19. Чертёж большого участка земной

поверхности:

а) географическая карта

б) аэрофотоснимок

в) космический снимок

г) план местности

20. Из предложенного списка выберите

три планеты земной группы:

а) Нептун

б) Марс

в) Меркурий

г) Юпитер

д) Уран

е) Венера

Показать ответ

Ответ:

У4КГРВ

22.08.2020 01:12

ответ:

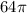$64\pi$ см³.

Объяснение:

Обозначим данную пирамиду буквами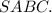 SABC.

AB = 12 см.

Проведём высоту пирамиды SO.

$\angle SAO = 30^{\circ}$

Начертим около этой пирамиды конус.

Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.

=======================================================

Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.

$\Rightarrow AB = BC = AC = 12$ см.

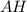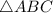
Проведём высоту в $\triangle ABC$

$\triangle SAO$ - прямоугольный, так как - высота пирамиды.

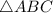$\triangle ABH$ - прямоугольный, так как - высота $\triangle ABC$ .

Так как $\triangle ABC$ - равносторонний ⇒ 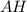- высота, медиана и биссектриса

BH = HC = BC:2 = 12:2 = 6 см, так как - медиана.

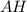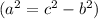Найдём по теореме Пифагора (a^2 = c^2 - b^2) .

$AH = \sqrt{AB^2 - BH^2} = \sqrt{12^2 - 6^2} = \sqrt{108} = 6\sqrt{3}$ см.

Точка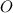 - пересечение медиан и делит их в отношении 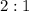2:1 , считая от вершины.

$\Rightarrow AO = 2/3\cdot AH = 2/3 \cdot 6\sqrt{3} = 4\sqrt{3}$ см

$OH = 1/3\cdot AH = 1/3 \cdot 6\sqrt{3} = 2\sqrt{3}$ см.

Также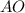 - радиус описанной около 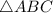$\triangle ABC$ окружности.

Рассмотрим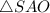 $\triangle SAO$

Если угол в прямоугольном треугольнике равен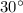 $30^{\circ}$ , то напротив лежащий катет равен половине гипотенузы.

$\Rightarrow SA = 2SO$

Составим уравнение:

Пусть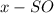 x - SO , тогда 2x - SA .

И по теореме Пифагора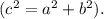 (c^2 = a^2 + b^2).

$(4\sqrt{3})^2 + x^2 = (2x)^2\\\\48 + x^2 = 4x^2\\\\-3x^2 =-48\\\\x^2 =16 \\\\x= 4$

конуса = $1/3 \cdot \pi \cdot AO^2 \cdot SO = \pi \Big(1/3 \cdot (4\sqrt{3})^2 \cdot 4\Big) = 64\pi$ см³.

Дана правильная треугольная пирамида со стороной основания 12. Боковое ребро пирамиды наклонено к пл

0,0(0 оценок)

Ответ:

proxiv

27.01.2023 07:25

Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Данный треугольник Пифагоров и гипотенуза равна 5см.

Точка М - центр описанной окружности.

Точка О - центр вписанной окружности.

Тогда R=2,5см, то есть ВМ=2,5см.

Радиус вписанной окружности равен по формуле:

r=(AC+BC-АВ)/2 = 2/2=1см.

Итак, СН=r=1см => HB=3-1=2см.

PB=HB=2см (касательные из одной точки).

Тогда МР=2,5-2=0,5см. В прямоугольном треугольнике ОМР по Пифагору:

ОМ=√(1²+0,5²)= √1,25 ≈ 1,118 ≈ 1,12см .

ответ: расстояние между центрами окружностей равно

√1,25 ≈ 1,12 см.

Или так: по теореме Эйлера в треугольнике расстояние между центрами вписанной и описанной окружностей находится по формуле:

d² = R² - 2·R·r.

В нашем случае R = 2,5см, а r = 1cм.

тогда d = √(2,5² -2·2,5) = √(2,5·0,5) = √1,25 ≈ 1,12 см.

Найдите расстояние между центрами вписанной и описанной окружностей прямоугольного треугольника с ка

0,0(0 оценок)

Популярные вопросы: Геометрия

привет929

22.10.2021 18:06

Периметр прямоугольного треугольника равен 72 метра. радиус вписанной в треугольник окружности 6 метров. найти диаметр описанной около треугольник окружности....

VladimirOwl

22.10.2021 18:06

Втреугольнике abc, где ab bc, проведена медиана bm. что больше: угол abm или угол cbm?...

usmanazamatov95

02.12.2020 05:09

Вравнобедренном треугольник abc с основанием bc...

ынпщщ357

02.12.2020 05:09

Стороны ав и вс треугольника авс равны соответственно 16 см и 22 см а высота проведенная к стороне ав равна 11 см найдите высоту проведенную к стороне вс...

дтш

02.12.2020 05:09

1)в прямоугольном треугольнике угол равен 30 градусов,а высота проведенная из вершины прямого угла равна корень из 3,найдите гипотенузу. 2)катеты прямоугольного треугольника...

Алина007485

02.12.2020 05:09

Треугольник абс прямоугольный угол а=60 угол с= 90ch высота треугольника = 8 смотрезок bk перпендикуляр к плоскости треугольника абс найти отрезок если расстояние от точки k...

xennika

02.12.2020 05:09

Основания трапеции равны 4см и 10см. найдите отрезки, на которые делит среднюю линию этой трапеции одна из её диагоналей....

mimikatja12

02.12.2020 05:09

Нужно окружность диаметром ав, где а (0; -2) в(8; 4) каким уравнением задаётся? ? 1) х2+(у+2)2=16 2) (х-4)2 + (у-1)2=25 3) х2+(у-4)2=16 4) (х+4)2+(у+1)2=25...

алик137

16.12.2021 10:26

Даны точки a(1; 1), b(4; 1), c(4; 5). найдите косинусы углов треугольника abc....

elyavlasova

27.02.2021 20:23

1. как найти точку пересечения диагоналей у ромба?...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку