Соч Геометрия 8 класс 1.Фигура, образованная конечным набором отрезков,расположенных так,что конец первого является концом второго,конец второго – началом третьего и т. д. А)Треугольник В)Ломаная С)квадрат Д)Прямоугольник 1б 2.Простая ломаная имеет 8 вершин. Сколько у нее сторон? А)6 В)8 С)7 Д)9 2б 3. На рисунке четырехугольник ABCD– ромб. Найдите угол А. A) 24 B) 39°; C) 54°; Д)62°; 1б 4. В параллелограмме ABCD угол A равен 55°. Высота BE делит сторону AD на две равные части. Найдите длину диагонали BD, если периметр параллелограмма равен 20 см. А)8 В)7 С)6 Д) 5 5б 5.Сторона АВ треугольника АВС равна 18 см. Сторона ВС разделена на 3 равные части и через точки деления проведены прямые, параллельные стороне АВ. Найдите длины отрезков этих прямых, содержащихся между сторонами треугольника. А)8 и 4 В)12 и 6 С)6 и 3 Д) 15 и 5 2 б 6. Средняя линия равнобедренного треугольника, параллельная основанию, равна 3 см. Найдите стороны треугольника, если его периметр равен 16 см. А) Основание 4см,боковые стороны по 7см В) Основание 5см,боковые стороны по 6см С)Основание 6см,боковые стороны по 5см Д) Основание 7см,боковые стороны по 4см 4 б 7. В равнобокой трапеции один из углов равен 110°, диагональ трапеции образует с основанием угол 29°. Найдите основания трапеции, если ее боковая сторона равна 7см. А)14 В)12 С)10 Д) 16

Показать ответ

Ответ:

astraelenap01fez

12.12.2022 19:41

Дано: КМРТ - прямокутник, КВ - бісектриса, ВР=5 см, МР+РТ+КТ+КМ=18 см. Знайти МК=РТ, МР=КТ.

МР+КМ=18:2=9 см. (це напівпериметр КМРТ)

ΔКМВ - рівнобедрений (∠МКВ=∠ВКТ=90:2=45°; ∠МВК=90-45=45°),

МК=МВ

МК+МВ=9-5=4 см; МК=2 см, МВ=2 см.

МК=РТ=2 см; МР=КТ=2+5=7 см.

Відповідь: 2 см, 7 см, 2 см, 7 см.

0,0(0 оценок)

Ответ:

JAHGH

22.11.2022 03:39

S треугольника всегда = высота*основание к которому она проведена разделить это всё на два. (h*осн.)/2

1) высота - 6, основание 12, значит площадь - 12*6/2= 72/2=36 - Б

2)Если в треугольнике есть угол в 30 градусов, то сторона напротив него - в два раза меньше гипотенузы ( стороны напротив прямого=90 угла).

Тут гипотенуза = 12 значит сторона напротив угла равна 12/2 = 6. Чтобы найти вторую сторону используем теорему Пифагора.

a^2+b^2=c^2

где а и б - стороны, а с - гипотенуза. Подставим известное...

6^2+b^2=12^2

36+B^2=144

b^2=144-36

b^2=108

b =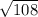 $\sqrt{108}$

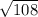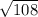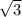Площадь треугольника здесь - 6* $\sqrt{108}$ /2 = 3* $\sqrt{108}$ =18 $\sqrt{3}$ -в

3)Опустим высоту. Найдём её тоже через свойство угла в 30 градусов и теорему пифагора. 16-4=12 значит высота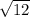 $\sqrt{12\\}$ . в итоге.

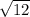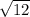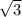площадь= $\sqrt{12}$ *6=6 $\sqrt{12}$ =12 $\sqrt{3}$ - в

4)Наименьшая высота будет опущена к самой большой стороне, запомни. Опустим ее к стороне 20. Через формулы ( набери в инете среднее геометрическое, долго оформлять очень ) найдём, что x=12,8 - кусочек, которой получается в результате деления высотой стороны двадцать, который ближе к стороне 16. Аналогично найдём и кусочек, ближний к стороне 12. y=7,2. Высота равна корню произведения xy= 9,6 - высота - г

0,0(0 оценок)

Популярные вопросы: Геометрия