Если это прямоугольный треугольник, то квадрат гипотенузы равен сумме квадратов катетов, исходя из его свойств. Нужно понять, какие единицы являются длинами катетов.
Если рассмотреть каждый случай, то очевидно, что длина катета равна 5(3²+4²=5², остальные равенства не выполняются).
Площадь прямоугольного треугольника равна половине произведения катетов
S = = 6
Есть второй через формулу Герона
Зная 3 стороны треугольника, найдём его полупериметр
3)Ребро в основании правильной шестиугольной пирамиды SABCDEF равно 4. Высота пирамиды SО равна 8.Найти расстояние от вершины А до середины бокового ребра SD.
Объяснение:
1) Пусть О-точка пересечения диагоналей ромба. По свойству диагоналей ромба О-середина АС .
О( (6+4):2 ; (7+3):2 ;(8+2):2) или О(5;5;5)
2)Вектор ВА (-1;2;0).
Точку D можно получить параллельным переносом на вектор ВА..
Тогда координаты D( 2+(-1) ;0+2;2+0) или D(1;2;2).
Пусть Н середина SD. Введем прямоугольную систему координат с началом в точке А и осью ох, совпадающей со стороной АD .Найдем координаты точек :А(0;0) , D(8;0) , S(4;8) .
Первый
Если это прямоугольный треугольник, то квадрат гипотенузы равен сумме квадратов катетов, исходя из его свойств. Нужно понять, какие единицы являются длинами катетов.
Если рассмотреть каждый случай, то очевидно, что длина катета равна 5(3²+4²=5², остальные равенства не выполняются).
Площадь прямоугольного треугольника равна половине произведения катетов
S =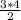 = 6
= 6
Есть второй через формулу Герона
Зная 3 стороны треугольника, найдём его полупериметр
p = 1/2 P = 1/2 (a+b+c) = 1/2 (3+4+5) = 12/2 =6
Формула Герона
S =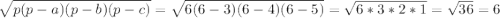
ответ: 6
1)2)-текст на фото.
3)Ребро в основании правильной шестиугольной пирамиды SABCDEF равно 4. Высота пирамиды SО равна 8.Найти расстояние от вершины А до середины бокового ребра SD.
Объяснение:
1) Пусть О-точка пересечения диагоналей ромба. По свойству диагоналей ромба О-середина АС .
О( (6+4):2 ; (7+3):2 ;(8+2):2) или О(5;5;5)
2)Вектор ВА (-1;2;0).
Точку D можно получить параллельным переносом на вектор ВА..
Тогда координаты D( 2+(-1) ;0+2;2+0) или D(1;2;2).
3) Основании правильной шестиугольной пирамиды-правильный шестиугольник ABCDEF ; а₆=R=4 , значит AD=8.
Пусть Н середина SD. Введем прямоугольную систему координат с началом в точке А и осью ох, совпадающей со стороной АD .Найдем координаты точек :А(0;0) , D(8;0) , S(4;8) .
Тогда координаты середины Н (6;4).
АН=√( (6-0)²+(4-0)²)=√52=4√13.