Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Объяснение:
Пусть ∠АLК=α
1) ΔАКL -прямоугольный, tg∠АLК= , AL=в / tgα.
2)ΔACD -прямоугольный, АС=а√2, по т. Пифагора.
ΔКCD -прямоугольный, по т. Пифагора, КС=√(а²+(а-в)²).
Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Объяснение:
Пусть ∠АLК=α
1) ΔАКL -прямоугольный, tg∠АLК= , AL=в / tgα.
, AL=в / tgα.
2)ΔACD -прямоугольный, АС=а√2, по т. Пифагора.
ΔКCD -прямоугольный, по т. Пифагора, КС=√(а²+(а-в)²).
3)ΔACК, угол ∠АСК=α.
По т. косинусов выразим cosα :
АК²=АС²+КС²-2АС*КС*cosα,
в²=2а²+а²+(а-в)²-2*а√2*√(а²+(а-в)²)*cosα,
2*а√2*√(а²+(а-в)²)*cosα =-в²+2а²+а²+(а-в)² ,
2*а√2*√(а²+(а-в)²)*cosα =-в²+4а²-2ав+в² ,
2*а√2*√(а²+(а-в)²)*cosα =2а(2а-в) ,
cosα =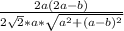
cosα = , tg²α=1:( cos²α)-1 , tgα =
, tg²α=1:( cos²α)-1 , tgα =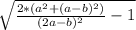 ,
,
tgα =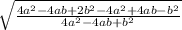 =
=
4)AL=в/tgα , AL=в: , AL=
, AL=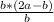 , AL=2a-b .
, AL=2a-b .