Проведём из центров окружностей О₁ и О₂ радиусы к точкам касания А и В. По свойству касательной О₁А = 8см и О₂В = 18см перпендикулярны АВ.
Межцентровое рассояние О₁О₂ = 8 + 18 = 26см
Из точки А проведём прямую АС параллельно О₁О₂. Получим параллелограмм АО₁О₂С, в котором О₂С = О₁А = 8см, а АС =О₁О₂ = 26см и тр-к АВС с прямым углом В
В этом тр-ке гипотенуза АС = О₁О₂ = 26см, катет ВС = О₂В - О₂С = 18 - 8 = 10см. АВ является катетом.
Проведём из центров окружностей О₁ и О₂ радиусы к точкам касания А и В. По свойству касательной О₁А = 8см и О₂В = 18см перпендикулярны АВ.
Межцентровое рассояние О₁О₂ = 8 + 18 = 26см
Из точки А проведём прямую АС параллельно О₁О₂. Получим параллелограмм АО₁О₂С, в котором О₂С = О₁А = 8см, а АС =О₁О₂ = 26см и тр-к АВС с прямым углом В
В этом тр-ке гипотенуза АС = О₁О₂ = 26см, катет ВС = О₂В - О₂С = 18 - 8 = 10см. АВ является катетом.
АВ² = АС² - ВС² = 26² - 10² = 676 - 100 = 576
АВ = 24
ответ: АВ = 24см
Обозначим призму буквами ABCA1B1C1, где ABC - нижнее основание, A1B1C1 - верхнее основание. Рассмотрим прямоугольный треугольнки ABC. Пусть угол ABC=90 градусов, угол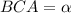
Сторона AC=c по условию задачи. Находим стороны AB и BC.
Так как AC - гипотенуза прямоугольного треугольника ABC, то большая боковая грань призмы - это AA1C1C. По условию угол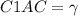
Рассмотрим треугольник C1AC. Он прямоугольный, так как призма - прямая. Угол C1CA=90 градусов. Находим сторону C1C:
Так как призма прямая, CC1=AA1=BB1
Теперь, когда мы знаем все стороны призмы, можно вычислить площадь поверхности. Площадь поверхности равна сумме площадей сторон призмы.
Площадь поверхности призмы равна: